题目内容
对n∈N*，不等式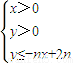
所表示的平面区域为Dn，把Dn内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成点列：（x1，y1），（x2，y2），（x3，y3），…，（xn，yn）．（1）求xn，yn；
（2）数列{an}满足a1=x1且n≥2时，
，求数列{an}的前n项和Sn；（3）设c1=1，当n≥2时，
，且数列{cn}的前n项和Tn，求T99．
【答案】分析：（1）画出可行域，结合图形写出xn，yn
（2）利用等比数列的前n项和公式求出an；利用错位相减法和等差数列的前n项和公式求出Sn
（3）先化简Cn，再利用裂项相消法求出T99
解答：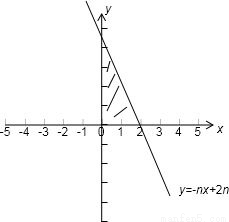
解：（1）
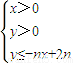的可行域为
如图示，xn=1，yn=n
（2）由题意可知：a1=1，an=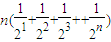
故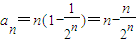
记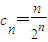
，则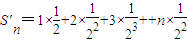
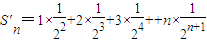
两式相减得：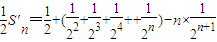
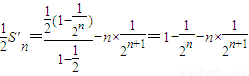
故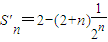
故数列{an}的前n项的和为：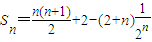
（3）当n≥2时，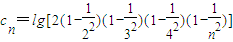
=
=
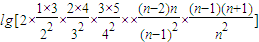
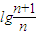=lg（n+1）-lgn
T99=1+（lg3-lg2）+（lg4-lg3）+（lg5-lg3）++（lg100-lg99）
=1+2-lg2
=3-lg2．
点评：本题考查画不等式组表示的平面区域；数列求和的方法：错位相减法、公式法、裂项相消法．
（2）利用等比数列的前n项和公式求出an；利用错位相减法和等差数列的前n项和公式求出Sn
（3）先化简Cn，再利用裂项相消法求出T99
解答：
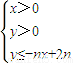解：（1）的可行域为如图示，xn=1，yn=n
（2）由题意可知：a1=1，an=
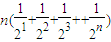
故
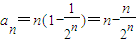
记
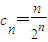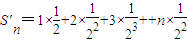
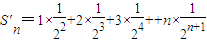
，则两式相减得：
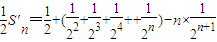
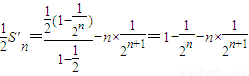
故
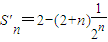
故数列{an}的前n项的和为：
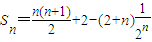
（3）当n≥2时，
=
=
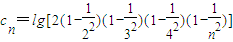
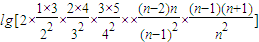
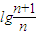=lg（n+1）-lgnT99=1+（lg3-lg2）+（lg4-lg3）+（lg5-lg3）++（lg100-lg99）
=1+2-lg2
=3-lg2．
点评：本题考查画不等式组表示的平面区域；数列求和的方法：错位相减法、公式法、裂项相消法．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
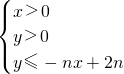所表示的平面区域为Dn，把Dn内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成点列：（x1，y1），（x2，y2），（x3，y3），…，（xn，yn）．
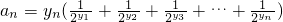，求数列{an}的前n项和Sn；
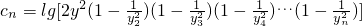，且数列{cn}的前n项和Tn，求T99．
所表示的平面区域为Dn，把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列：(x1，y1)，(x2，y2)，(x3，y4)，…，(xn,yn)
(
).证明当n≥2时,
；
)·(1+
)·(1+
)…(1+
)与4的大小关系.
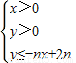所表示的平面区域为Dn，把Dn内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成点列：（x1，y1），（x2，y2），（x3，y3），…，（xn，yn）．
，求数列{an}的前n项和Sn；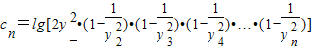
，且数列{cn}的前n项和Tn，求T99．
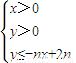所表示的平面区域为Dn，把Dn内的整点（横坐标与纵坐标均为整数的点）按其到原点的距离从近到远排成点列：（x1，y1），（x2，y2），（x3，y3），…，（xn，yn）．
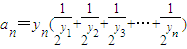，求数列{an}的前n项和Sn；
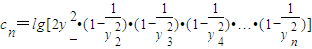，且数列{cn}的前n项和Tn，求T99．