题目内容
对n∈N*,不等式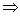 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)(Ⅰ)求xn,yn;
(Ⅱ)数列{an}满足a1=x1,且n≥2时an=![]() (
(![]() ).证明当n≥2时,
).证明当n≥2时,![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,试比较(1+![]() )·(1+
)·(1+![]() )·(1+
)·(1+![]() )…(1+
)…(1+![]() )与4的大小关系.
)与4的大小关系.
解:(Ⅰ)-nx+2n>0![]() x<2,又x>0且x∈N*,∴x=1
x<2,又x>0且x∈N*,∴x=1
故Dn内的整点都落在直线x=1上且y≤n,故Dn内的整点按其到原点的距离从近到远排成的点列为:(1,1),(1,2),(1,3),…,(1,n),∴xn=1,yn=n.
(Ⅱ)证:当n≥2时,由an=![]() ,
,
得![]() ,即=
,即=![]() ①
①
∴![]() ②
②
②式减①式,有![]() ,得证.
,得证.
(Ⅲ)解:当n=1时,l+![]() =2<4;当n=2时,(1+
=2<4;当n=2时,(1+![]() )(1+
)(1+![]() )=2×<4,
)=2×<4,
由(Ⅱ)知,当n≥2时,![]()
∴当n≥3时,![]()
=![]() (1+an)
(1+an)
=![]()
![]()
∵![]() (n≥2),
(n≥2),
∴上式<2[1+(1![]() )
)![]() ]=2(2
]=2(2![]() )=4
)=4![]() <4,
<4,
∴(1+![]() )·(1+
)·(1+![]() )·(1+
)·(1+![]() )…(1+
)…(1+![]() )<4.
)<4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
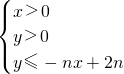 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).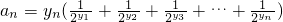 ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;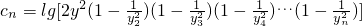 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.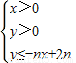 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn). ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;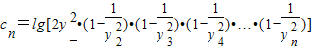 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.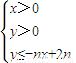 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).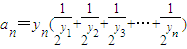 ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;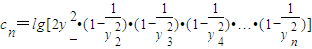 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.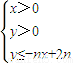 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn). ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn; ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.