题目内容
11.已知正三角形内切圆的半径是高的$\frac{1}{3}$,把这个结论推广到正四面体,类似的结论正确的是( )| A. | 正四面体的内切球的半径是高的$\frac{1}{2}$ | B. | 正四面体的内切球的半径是高的$\frac{1}{3}$ | ||
| C. | 正四面体的内切球的半径是高的$\frac{1}{4}$ | D. | 正四面体的内切球的半径是高的$\frac{1}{6}$ |
分析 连接球心与正四面体的四个顶点.把正四面体分成四个高为r的三棱锥,正四面体的体积,就是四个三棱锥的体积的和,求解即可.
解答 解:如图示: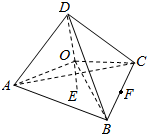
球心到正四面体一个面的距离即球的半径r,连接球心与正四面体的四个顶点.
把正四面体分成四个高为r的三棱锥,所以4×$\frac{1}{3}$S×r=$\frac{1}{3}$×S×h,r=$\frac{1}{4}$h,
(其中S为正四面体一个面的面积,h为正四面体的高)
故选:C.
点评 本题考查类比推理,解题的关键是明确类比的方法,明确正三角形面积、正四面体体积的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.我们知道,在边长为a的正三角形内任一点到三边的距离之和为定值$\frac{{\sqrt{3}}}{2}a$,类比上述结论,在棱长为a的正四面体内任一点到其四个面的距离之和为定值,此定值为( )
| A. | $\frac{{\sqrt{6}}}{3}a$ | B. | $\frac{{\sqrt{5}}}{2}a$ | C. | $\frac{{2\sqrt{2}}}{3}a$ | D. | a |
3.锐角△ABC中,已知$a=\sqrt{3},A=\frac{π}{3}$,则b2+c2+bc的取值范围是( )
| A. | (3,9] | B. | (5,9] | C. | (7,9] | D. | (5,7] |