题目内容
17.已知抛物线y2=-2px的准线与圆x2+y2-6x+8=0相切,则p的值为4或8.分析 将圆化成标准方程,得到圆心为C(3,0),半径r=1.再将抛物线化成标准方程,得到抛物线的准线为x=-$-\frac{p}{2}$,根据准线与圆相切建立关于p的等式,解之即可得到p的值.
解答 解:圆x2+y2-6x+8=0化成标准方程,得(x-3)2+y2=1,
∴圆心为C(3,0),半径r=1,
又∵抛物线y2=-2px(p>0)
∴抛物线的准线为x=$\frac{p}{2}$,
∵抛物线的准线与圆相切,
∴准线到圆心C的距离等于半径,得|3-$\frac{p}{2}$|=1,解之得p=4或p=8.
故答案为:4或8.
点评 本题给出抛物线的准线与已知圆相切,求p的值.着重考查了圆的标准方程、直线与圆的位置关系和抛物线的标准方程与简单性质等知识,属于中档题..

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
8.已知函数f(x)=loga(x2+1)(a>0)在[0,1]上的最大值为1,函数g(x)=($\frac{1}{3}$)x-m,若?x1∈[0,3],?x2∈[1,2],使得f(x1)≥g(x2),则实数m的取值范围是( )
| A. | [$\frac{1}{9}$,+∞) | B. | [$\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{9}$] | D. | (-∞,$\frac{1}{3}$] |
5.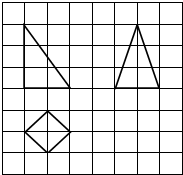 如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )| A. | $\sqrt{2}$+$\sqrt{6}$ | B. | 2+2$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+2$\sqrt{6}$ | D. | 2+3$\sqrt{2}$+$\sqrt{22}$ |
5.设经过定点P(a,0)的直线与抛物线y2=6x相交于A,B两点,若$\frac{1}{|PA{|}^{2}}+\frac{1}{|PB{|}^{2}}$为定值,则a=( )
| A. | 6 | B. | 3 | C. | $\frac{3}{2}$ | D. | 1 |