题目内容
14．在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，且在两种坐标系中取相同的单位长度，将点P的极坐标（2，$\frac{π}{4}$）化成直角坐标（$\sqrt{2}$，$\sqrt{2}$）．分析 设P（x，y），由公式x=ρcosθ、y=ρsinθ和条件可得答案．
解答 解：设点（2，$\frac{π}{4}$）的直角坐标是（x，y），
由题意得，x=2cos$\frac{π}{4}$=$\sqrt{2}$，y=2sin$\frac{π}{4}$=$\sqrt{2}$，
所以点（2，$\frac{π}{4}$）的直角坐标是（$\sqrt{2}$，$\sqrt{2}$）．
故答案为：（$\sqrt{2}$，$\sqrt{2}$）．
点评 本题考查极坐标与直角坐标的互化，掌握相关转化公式是解题的关键，属于基础题．
练习册系列答案
相关题目
5．
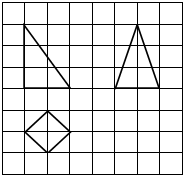如图，网格纸上小正方形的边长为1，粗实线画出的是某底面为正方形的四棱锥的三视图，则该四棱锥的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某底面为正方形的四棱锥的三视图，则该四棱锥的表面积为（ ）| A． | $\sqrt{2}$+$\sqrt{6}$ | B． | 2+2$\sqrt{6}$ | C． | 2+2$\sqrt{2}$+2$\sqrt{6}$ | D． | 2+3$\sqrt{2}$+$\sqrt{22}$ |
5．设经过定点P（a，0）的直线与抛物线y2=6x相交于A，B两点，若$\frac{1}{|PA{|}^{2}}+\frac{1}{|PB{|}^{2}}$为定值，则a=（ ）
| A． | 6 | B． | 3 | C． | $\frac{3}{2}$ | D． | 1 |
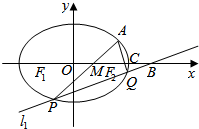已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点为F1、F2，且椭圆E过点（0，$\sqrt{3}$），（$\sqrt{3}$，-$\frac{\sqrt{6}}{2}$），点A是椭圆上位于第一象限的一点，且△AF1F2的面积S△${\;}_{A{F}_{1}{F}_{2}}$=$\sqrt{3}$．