题目内容
 中,
中, ,则此三角形解的情况是 ( )
,则此三角形解的情况是 ( )
| A.一个解 | B.两个解 | C.无解 | D.不能确定 |
A
解析试题分析:因为 ,且a>b,所以此三角形有一个解。
,且a>b,所以此三角形有一个解。
考点:三角形解得个数的判断。
点评:正弦定理通常用来解决:①已知两角和任一边,求另一角和其他两边;②已知两边和其中一边的对角,求另一边和其他两角。对于②这种类型的题,一定要注意判断解的个数,其实这种情况下用余弦定理更好些,可以免掉判断解的个数。

练习册系列答案
相关题目
若 的内角
的内角 所对的边
所对的边 满足
满足 ,且
,且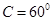 ,则
,则  的值为( )
的值为( )
A. | B. 1 1 | C. | D. |
在△ABC中,角A,B,C所对的边分别是a,b,c,若 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等腰或直角三角形 |
在△ABC中,若 ,则△ABC的形状是
,则△ABC的形状是
| A.直角三角形 | B.等腰或直角三角形 | C.等腰三角形 | D.不能确定 |
在已知 ABC的内角
ABC的内角 的对边
的对边 若a=csinA则
若a=csinA则 的最大值为( )
的最大值为( )
A. | B.1 | C. | D. |
 中,角
中,角 、
、 、
、 所以的边为
所以的边为 、
、 、
、 , 若
, 若 ,
, ,
, 面积
面积 ,则
,则 ( )
( )
A. | B. | C. | D. |
 的内角
的内角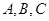 所对的边分别为
所对的边分别为 ,
, ,
, ,
, ,则此三角形( )
,则此三角形( )
| A.一定是锐角三角形 |
| B.一定是直角三角形 |
| C.一定是钝角三角形 |
| D.可能是钝角三角形,也可能是锐角三角形 |
 ] B.(0,
] B.(0, ]
] ,则角A等于( )
,则角A等于( )


