题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c,若 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等腰或直角三角形 |
D
解析试题分析:利用正弦定理化简acosA=bcosB,通过两角差的正弦函数,求出A与B的关系,得到三角形的形状.解:在△ABC中,∠A,∠B,∠C所对边分别为a,b,c,若a cosA=b cosB,所以sinAcosA=sinBcosB,所以2A=2B或2A=π-2B,所以A=B或A+B=90°.所以三角形是等腰三角形或直角三角形.故答案为:等腰三角形或直角三角形.
考点:正弦定理
点评:本题是基础题,考查正弦定理在三角形中的应用,三角形的形状的判断,考查计算能力.

练习册系列答案
相关题目
 中,三边长
中,三边长 满足
满足 ,那么
,那么 的形状为( )
的形状为( )
| A.锐角三角形 | B.钝角三角形 | C.直角三角形 | D.以上均有可能 |
在△ABC中,若∠A∶∠B∶∠C=1∶2∶3,则a∶b∶c等于
| A.1∶2∶3 | B.3∶2∶1 | C. | D. |
在△ABC中,若sin2A+sin2B<sin2C,则△ABC的形状是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不能确定 |
在△ABC中,a=3,b= ,c=2,那么B等于
,c=2,那么B等于
| A.30° | B.45° | C.60° | D.120° |
 中,
中, ,则此三角形解的情况是 ( )
,则此三角形解的情况是 ( )
| A.一个解 | B.两个解 | C.无解 | D.不能确定 |
在 中边
中边 ,
,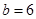 ,
, ,则
,则 面积是( )
面积是( )
| A.6 | B. | C.12 | D. |
 (a、b、c分别为角A、B、C的对边),则△ABC的形状为( )
(a、b、c分别为角A、B、C的对边),则△ABC的形状为( )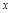 km,再朝西偏北
km,再朝西偏北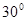 的方向走了3km,结果它离出发点恰好为
的方向走了3km,结果它离出发点恰好为 km,那么
km,那么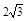 C.3 D.
C.3 D.