题目内容
在已知 ABC的内角
ABC的内角 的对边
的对边 若a=csinA则
若a=csinA则 的最大值为( )
的最大值为( )
A. | B.1 | C. | D. |
D
解析试题分析:根据正弦定理及a=csinA求得C.进而根据勾股定理可知c2=a2+b2,对 的平方化简整理
的平方化简整理
根据基本不等式得到的范围,进而得出答案。解:a=csinA,得到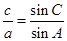 =sinA.所以sinC=1,即C=90°.所以c2=a2+b2.
=sinA.所以sinC=1,即C=90°.所以c2=a2+b2.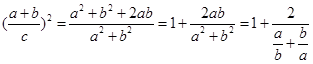 ,然后根据均值不等式可知结论分母有最小值为2,整个表达式有最大值为2,那么可知
,然后根据均值不等式可知结论分母有最小值为2,整个表达式有最大值为2,那么可知 的最大值为
的最大值为 ,选D
,选D
考点:正弦定理
点评:本题主要考查正弦定理和基本不等式在解三角形中的应用

练习册系列答案
相关题目
如图,要测出山上石油钻井的井架 的高,从山脚
的高,从山脚 测得
测得 m, 塔顶
m, 塔顶 的仰角
的仰角 ,塔底
,塔底 的仰角
的仰角 ,则井架的高
,则井架的高 为( )
为( ) 
A. m m | B. m m | C. m m | D. m m |
在△ABC中,若sin2A+sin2B<sin2C,则△ABC的形状是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不能确定 |
在△ABC中,a=3,b= ,c=2,那么B等于
,c=2,那么B等于
| A.30° | B.45° | C.60° | D.120° |
 中,
中, ,则此三角形解的情况是 ( )
,则此三角形解的情况是 ( )
| A.一个解 | B.两个解 | C.无解 | D.不能确定 |
在 中边
中边 ,
,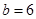 ,
, ,则
,则 面积是( )
面积是( )
| A.6 | B. | C.12 | D. |
在△ABC中,已知b=4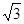 ,c=2
,c=2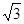 ,∠A=120°,则a等于 ( )
,∠A=120°,则a等于 ( )
A. | B.6 | C.2 或6 或6 | D.2 |
 ,则
,则 =( )
=( )  B.
B.  C.
C. D.
D.