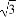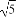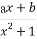题目内容
已知函数f(x)= x3-
x3-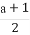 x2+x+b,其中a,b∈R.
x2+x+b,其中a,b∈R.
(1)若曲线y=f(x)在点P(2,f(2))处的切线方程为y=5x-4,求函数f(x)的解析式.
(2)当a>0时,讨论函数f(x)的单调性.
(1) f(x)=x3-2x2+x+4
(2) 当0<a<1时, >1,函数f(x)在区间(-∞,1)及(
>1,函数f(x)在区间(-∞,1)及( ,+∞)上为增函数,在区间(1,
,+∞)上为增函数,在区间(1, )上为减函数;
)上为减函数;
当a=1时, =1,函数f(x)在区间(-∞,+∞)上为增函数;
=1,函数f(x)在区间(-∞,+∞)上为增函数;
当a>1时, <1,函数f(x)在区间(-∞,
<1,函数f(x)在区间(-∞, )及(1,+∞)上为增函数,在区间(
)及(1,+∞)上为增函数,在区间( ,1)上为减函数.
,1)上为减函数.
【解析】(1)f'(x)=ax2-(a+1)x+1.
由导数的几何意义得f'(2)=5,于是a=3.
由切点P(2,f(2))在直线y=5x-4上可知2+b=6,解得b=4.
所以函数f(x)的解析式为f(x)=x3-2x2+x+4.
(2)f'(x)=ax2-(a+1)x+1=a(x- )(x-1).
)(x-1).
当0<a<1时, >1,函数f(x)在区间(-∞,1)及(
>1,函数f(x)在区间(-∞,1)及( ,+∞)上为增函数,在区间(1,
,+∞)上为增函数,在区间(1, )上为减函数;
)上为减函数;
当a=1时, =1,函数f(x)在区间(-∞,+∞)上为增函数;
=1,函数f(x)在区间(-∞,+∞)上为增函数;
当a>1时, <1,函数f(x)在区间(-∞,
<1,函数f(x)在区间(-∞, )及(1,+∞)上为增函数,在区间(
)及(1,+∞)上为增函数,在区间( ,1)上为减函数.
,1)上为减函数.

练习册系列答案
相关题目