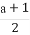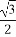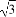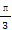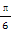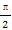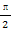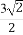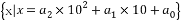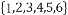题目内容
给出如下五个结论:
①存在α∈(0,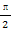
),使sinα+cosα=
;
②存在区间(a,b),使y=cosx为减函数而sinx<0;
③y=tanx在其定义域内为增函数;
④y=cos2x+sin(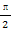-x)既有最大值和最小值,又是偶函数;
⑤y=sin|2x+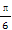
|的最小正周期为π.
其中正确结论的序号是 .
④
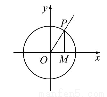
【解析】①中α∈(0,
)时,如图,由三角函数线知OM+MP>1,得sinα+cosα>1,故①错.
②由y=cosx的减区间为(2kπ,2kπ+π)(k∈Z),故sinx>0,因而②错.
③正切函数的单调区间是(kπ-,kπ+),k∈Z.
故y=tanx在定义域内不单调,故③错.
④y=cos2x+sin(-x)=cos2x+cosx
=2cos2x+cosx-1=2(cosx+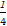
)2-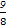
.
ymax=2,ymin=-.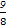
故函数既有最大值和最小值,又是偶函数,故④正确.
⑤结合图象可知y=sin|2x+
|不是周期函数,故⑤错.
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
