Question

（本小题满分16分）

随机抽取某厂的某种产品400件，经质检，其中有一等品252件、二等品100件、三等品40件、次品8件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润（单位：万元）为

（1）求的分布列和数学期望

（2）经技术革新后，仍有四个等级的产品，但次品率降为，一等品率提高为．如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？

 

 

Answer 1

【答案】

 

	6	2	1	-2
	0.63	0.25	0.1	0.02

，

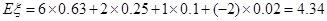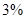
【解析】解：(1)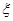的所有可能取值有6，2，1，-2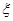； 的分布列为：

	6	2	1	-2
	0.63	0.25	0.1	0.02

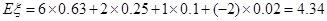………………………10分

（2）设技术革新后的三等品率为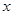，则此时1件产品的平均利润为

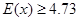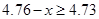，即，解得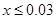，三等品率最多为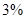…………16分