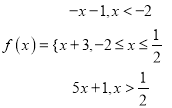题目内容
【题目】在公比为q的等比数列{an}中，已知a1＝16，且a1，a2＋2，a3成等差数列．
(Ⅰ)求q，an；
(Ⅱ)若q＜1，求满足a1－a2＋a3－…＋(－1)2n－1a2n>10的最小的正整数n的值．
【答案】(Ⅰ)见解析(Ⅱ)3.
【解析】试题分析：（1）由a1，a2＋2，a3成等差数列，可求得公比q，an。（2）由（1）及q＜1，可得，an＝25－n，可得原不等式左边是等比数列数列
求和。
试题解析：(Ⅰ)由16＋16q2＝2(16q＋2)得4q2－8q＋3＝0，q＝
或
，
当q＝
时，an＝25－n，
当q＝
时，an＝16(
)n－1.
(Ⅱ)q＜1，an＝25－n，a1－a2＋a3＋…＋(－1)2n－1a2n＝
＝
[
]>10，
(
)2n< 
，2n>4，n>2，正整数n的最小值为3.
练习册系列答案
学业测评一课一测系列答案
相关题目
