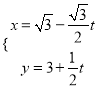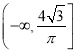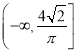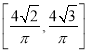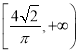题目内容
【题目】在直角坐标系xOy中,曲线M的参数方程为![]() (θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+
(θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+![]() )=
)=![]() t(其中t为常数).
t(其中t为常数).
(Ⅰ)若曲线N与曲线M只有一个公共点,求t的值;
(Ⅱ)当t=-1时,求曲线M上的点与曲线N上的点的最小距离.
【答案】(Ⅰ) t=3±![]() (Ⅱ)2
(Ⅱ)2![]() -1.
-1.
【解析】试题分析:(1)由曲线M的参数方程化普通方程可得)M:(x-1)2+(y-2)2=1,由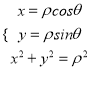 可得曲线N的普通方程N:x+y=t,由题意可得直线与圆相切,即圆心到直线距离等于半径,可求得t。(2) 当t=-1时,由圆心到直线的距离减去半径即为两点距离最小值。
可得曲线N的普通方程N:x+y=t,由题意可得直线与圆相切,即圆心到直线距离等于半径,可求得t。(2) 当t=-1时,由圆心到直线的距离减去半径即为两点距离最小值。
试题解析:(Ⅰ)M可化为(x-1)2+(y-2)2=1,N可化为x+y=t.
由![]() 得t=3±
得t=3±![]() .
.
(Ⅱ)当t=-1时,直线N:x+y=-1,圆M的圆心到直线N距离d=![]() =2
=2![]() >1,
>1,
∴曲线M上的点到曲线N上的点的最小距离为2![]() -1.
-1.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目