题目内容
圆x2+y2-4x=0,在点P(1, )处的切线方程为
)处的切线方程为
- A.x+y-2=0
- B.x+y-4=0
- C.x-y+4=0
- D.x-y+2=0
D
分析:由圆的方程找出圆心坐标和圆的半径,根据圆的切线垂直于过切点的直径,由圆心和P的坐标求出OP确定直线方程的斜率,根据两直线垂直时斜率乘积为-1,求出切线的斜率,根据M坐标和求出的斜率写出切线方程即可.
解答:点(1, )在圆x2+y2-4x=0上,圆心坐标(2,0),半径为:2,
)在圆x2+y2-4x=0上,圆心坐标(2,0),半径为:2,
∴点P为切点,从而圆心与P的连线应与切线垂直,
又∵圆心为(2,0),∴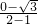 •k=-1,
•k=-1,
解得k= ,即切线方程为x-y+2=0.
,即切线方程为x-y+2=0.
故选D.
点评:此题考查学生掌握点与圆的位置关系及直线与圆的位置关系,掌握两直线垂直时斜率所满足的关系,会根据一点的坐标和直线的斜率写出直线的方程,是一道综合题.
分析:由圆的方程找出圆心坐标和圆的半径,根据圆的切线垂直于过切点的直径,由圆心和P的坐标求出OP确定直线方程的斜率,根据两直线垂直时斜率乘积为-1,求出切线的斜率,根据M坐标和求出的斜率写出切线方程即可.
解答:点(1,
 )在圆x2+y2-4x=0上,圆心坐标(2,0),半径为:2,
)在圆x2+y2-4x=0上,圆心坐标(2,0),半径为:2,∴点P为切点,从而圆心与P的连线应与切线垂直,
又∵圆心为(2,0),∴
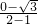 •k=-1,
•k=-1,解得k=
 ,即切线方程为x-y+2=0.
,即切线方程为x-y+2=0.故选D.
点评:此题考查学生掌握点与圆的位置关系及直线与圆的位置关系,掌握两直线垂直时斜率所满足的关系,会根据一点的坐标和直线的斜率写出直线的方程,是一道综合题.

练习册系列答案
相关题目
圆x2+y2-4x+4y+6=0截直线x-y-5=0所得的弦长等于( )
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、5 |