题目内容
(本小题满分14分)
已知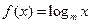 (
(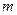 为常数,
为常数,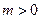 且
且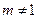 ),设
),设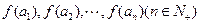 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
(1)求证:数列{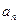 }是等比数列;
}是等比数列;
(2)若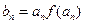 ,记数列
,记数列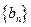 的前n项和为
的前n项和为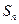 ,当
,当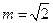 时,求
时,求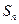 ;
;
(3)若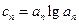 ,问是否存在实数
,问是否存在实数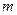 ,使得
,使得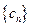 中每一项恒小于它后面的项?
中每一项恒小于它后面的项?
若存在,求出实数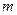 的取值范围.
的取值范围.
已知
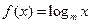 (
(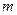 为常数,
为常数,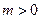 且
且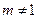 ),设
),设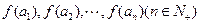 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列. (1)求证:数列{
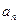 }是等比数列;
}是等比数列;(2)若
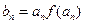 ,记数列
,记数列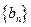 的前n项和为
的前n项和为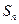 ,当
,当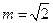 时,求
时,求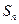 ;
;(3)若
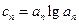 ,问是否存在实数
,问是否存在实数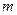 ,使得
,使得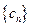 中每一项恒小于它后面的项?
中每一项恒小于它后面的项?若存在,求出实数
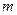 的取值范围.
的取值范围.解:(1)由题意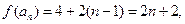 即
即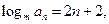
∴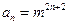 ………………2分
………………2分
∴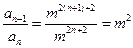 ∵m>0且
∵m>0且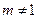 ,∴m2为非零常数,
,∴m2为非零常数,
∴数列{an}是以m4为首项,m2为公比的等比数列 …………4分
(2)由题意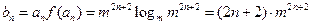 ,
,
当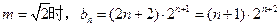
∴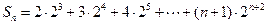 ① …………6分
① …………6分
①式乘以2,得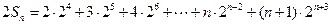 ② …7分
② …7分
②-①并整理,得
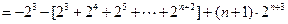
=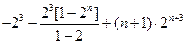
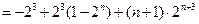
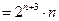 ……… 10分
……… 10分
(3)由题意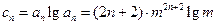 ,要使
,要使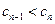 对一切
对一切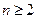 成立,
成立,
即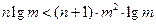 对一切
对一切 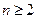 成立,
成立,
①当m>1时,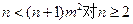 成立; …………12分
成立; …………12分
②当0<m<1时,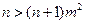
∴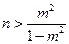 对一切
对一切 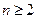 成立,只需
成立,只需 ,
,
解得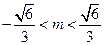 , 考虑到0<m<1, ∴0<m<
, 考虑到0<m<1, ∴0<m<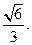
综上,当0<m<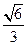 或m>1时,数列
或m>1时,数列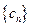 中每一项恒小于它后面的项…………14分
中每一项恒小于它后面的项…………14分
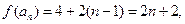 即
即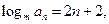
∴
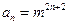 ………………2分
………………2分∴
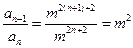 ∵m>0且
∵m>0且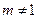 ,∴m2为非零常数,
,∴m2为非零常数,∴数列{an}是以m4为首项,m2为公比的等比数列 …………4分
(2)由题意
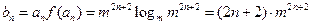 ,
,当
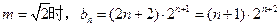
∴
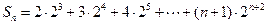 ① …………6分
① …………6分①式乘以2,得
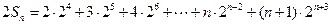 ② …7分
② …7分②-①并整理,得

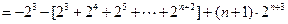
=
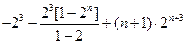
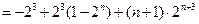
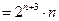 ……… 10分
……… 10分(3)由题意
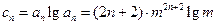 ,要使
,要使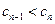 对一切
对一切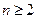 成立,
成立,即
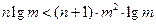 对一切
对一切 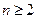 成立,
成立,①当m>1时,
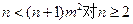 成立; …………12分
成立; …………12分②当0<m<1时,
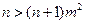
∴
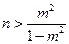 对一切
对一切 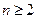 成立,只需
成立,只需 ,
,解得
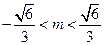 , 考虑到0<m<1, ∴0<m<
, 考虑到0<m<1, ∴0<m<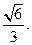
综上,当0<m<
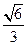 或m>1时,数列
或m>1时,数列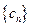 中每一项恒小于它后面的项…………14分
中每一项恒小于它后面的项…………14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
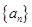 的公差大于0,且
的公差大于0,且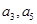 是方程
是方程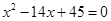 的两根,数列
的两根,数列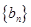 的前
的前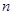 项的和为
项的和为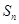 ,且
,且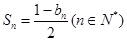 .
.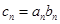 ,求数列
,求数列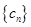 的前
的前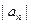 ,
,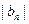 中,a1=2,b1=4,且
中,a1=2,b1=4,且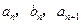 成等差数列,
成等差数列,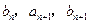 成等比数列(
成等比数列(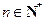 )
) 2,b3,b4,由此猜测
2,b3,b4,由此猜测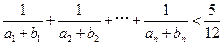 .
.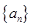 中,
中,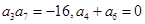 ,求
,求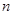 项和
项和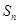 。
。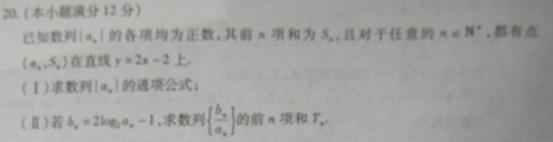
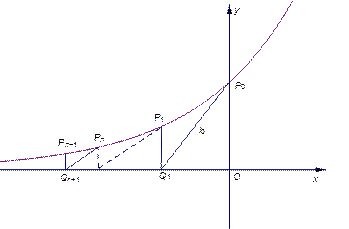
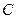 :
: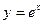 上一点
上一点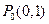 作曲线
作曲线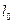 交
交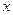 轴于点
轴于点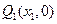 ,又过
,又过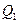 作
作 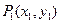 ,然后再过
,然后再过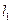 交
交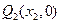 ,又过
,又过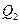 作
作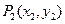 ,
, ,以此类推,过点
,以此类推,过点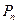 的切线
的切线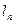 与
与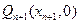 ,再过点
,再过点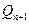 作
作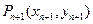 (
(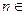 N
N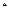 ).
).
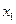 、
、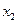 及数列
及数列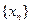 的通项公式;
的通项公式;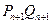 所围成的图形面积为
所围成的图形面积为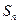 ,求
,求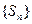 的前
的前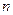 项和为
项和为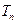 ,求证:
,求证: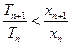
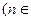 N
N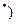 .
.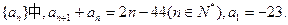
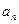 ;(2)设
;(2)设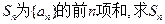 的最小值。
的最小值。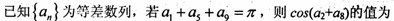

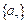 满足递推式:
满足递推式: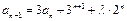 ,若数列
,若数列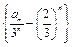 为等差数列,则实数
为等差数列,则实数 =" " .
=" " .