题目内容
20.已知|$\overrightarrow{a}$|=8,|$\overrightarrow{b}$|=15.(1)求|$\overrightarrow{a}$-$\overrightarrow{b}$|的取值范围;
(2)若|$\overrightarrow{a}$-$\overrightarrow{b}$|=17,则表示$\overrightarrow{a}$、$\overrightarrow{b}$的有向线段所在的直线所成的角是多少?
分析 (1)运用两向量模的不等式||$\overrightarrow{a}$|-|$\overrightarrow{b}$||≤|$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,即可得到所求范围;
(2)可设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{CB}$=$\overrightarrow{a}$-$\overrightarrow{b}$,|$\overrightarrow{CB}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=17,两边平方计算即可得到$\overrightarrow{a}$⊥$\overrightarrow{b}$.
解答 解:(1)由||$\overrightarrow{a}$|-|$\overrightarrow{b}$||≤|$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,
即有7≤|$\overrightarrow{a}$-$\overrightarrow{b}$|≤23,
即为|$\overrightarrow{a}$-$\overrightarrow{b}$|的取值范围无[7,23];
(2)由于|$\overrightarrow{a}$-$\overrightarrow{b}$|=17,|$\overrightarrow{a}$|=8,|$\overrightarrow{b}$|=15,
可设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,
则$\overrightarrow{CB}$=$\overrightarrow{a}$-$\overrightarrow{b}$,|$\overrightarrow{CB}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}}$
=$\sqrt{{8}^{2}+1{5}^{2}-2\overrightarrow{a}•\overrightarrow{b}}$=17,
解得$\overrightarrow{a}$$•\overrightarrow{b}$=0,即有$\overrightarrow{a}$⊥$\overrightarrow{b}$,
即有表示$\overrightarrow{a}$、$\overrightarrow{b}$的有向线段所在的直线所成的角是90°.
点评 本题考查向量的模的不等式和向量的加减运算和数量积的性质,属于中档题.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案| ξ | 1 | 2 | 3 | 4 | 5 |
| P | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |
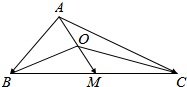 如图,在△ABC中,O为中线AM上的动点.
如图,在△ABC中,O为中线AM上的动点.