Question

10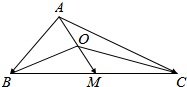．如图，在△ABC中，O为中线AM上的动点．
（1）证明：$\overrightarrow{OB}$+$\overrightarrow{OC}$=2$\overrightarrow{OM}$
（2）设|$\overrightarrow{AM}$|=2，$\overrightarrow{OM}$=t$\overrightarrow{AM}$（0≤t≤1），试把$\overrightarrow{OA}$•（$\overrightarrow{OB}+\overrightarrow{OC}$）表示为t的函数f（t），并求当O在AM上何处时，f（t）的值最小，最小值是多少？

Answer 1

分析 （1）延长OM到D使得MD=OM，由平行四边形法则可得：$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OD}$=2$\overrightarrow{OM}$，即可证明．
（2）由（1）可得：$\overrightarrow{OB}$+$\overrightarrow{OC}$=2$\overrightarrow{OM}$．又$\overrightarrow{OM}$=t$\overrightarrow{AM}$（0≤t≤1），可得$\overrightarrow{OA}=（t-1）•\overrightarrow{AM}$．于是f（t）=2$\overrightarrow{OA}•\overrightarrow{AM}$=2$（t-1）{\overrightarrow{AM}}^{2}$=8t-8，利用一次函数的单调性即可得出．

解答 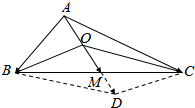（1）证明：延长OM到D使得MD=OM，∵O为中线AM上的动点，
由平行四边形法则可得：$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{OD}$=2$\overrightarrow{OM}$，∴$\overrightarrow{OB}$+$\overrightarrow{OC}$=2$\overrightarrow{OM}$．
（2）解：由（1）可得：$\overrightarrow{OB}$+$\overrightarrow{OC}$=2$\overrightarrow{OM}$．
又$\overrightarrow{OM}$=t$\overrightarrow{AM}$（0≤t≤1），
∴$\overrightarrow{OA}+\overrightarrow{AM}$=t$\overrightarrow{AM}$，化为$\overrightarrow{OA}=（t-1）•\overrightarrow{AM}$．
已知|$\overrightarrow{AM}$|=2，
∴f（t）=$\overrightarrow{OA}$•（$\overrightarrow{OB}+\overrightarrow{OC}$）=2$\overrightarrow{OA}•\overrightarrow{AM}$=2$（t-1）{\overrightarrow{AM}}^{2}$=8t-8，
∴当t=0时，f（t）取得最小值-8．
此时O与点M重合．

点评 本题考查了向量的平行四边形法则、三角形法则、共线定理、一次函数的单调性，考查了推理能力与计算能力，属于中档题．