题目内容
(本小题满分12分)如图,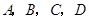 为空间四点.在
为空间四点.在 中,
中, .等边三角形
.等边三角形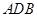 以
以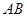 为轴运动.
为轴运动.
(1)当平面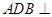 平面
平面 时,求
时,求 ;
;
(2)当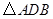 转动时,证明总有
转动时,证明总有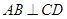 ?
?
(1)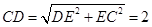 . (2)证明:见解析。
. (2)证明:见解析。
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
(本小题满分12分)如图,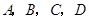 为空间四点.在
为空间四点.在 中,
中, .等边三角形
.等边三角形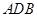 以
以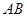 为轴运动.
为轴运动.
(1)当平面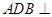 平面
平面 时,求
时,求 ;
;
(2)当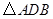 转动时,证明总有
转动时,证明总有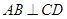 ?
?
(1)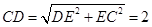 . (2)证明:见解析。
. (2)证明:见解析。
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案