题目内容
(本小题满分12分)如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠DAB=60°.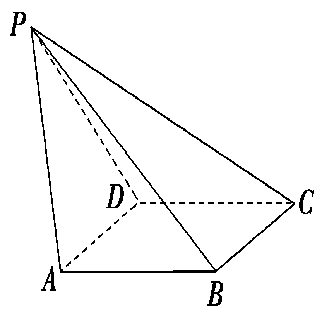
(1)证明:∠PBC=90°;
(2)若PB=3,求直线AB与平面PBC所成角的正弦值.
(1)取AD中点O,连OP、OB,由已知得:OP⊥AD,OB⊥AD,
又OP∩OB=O,∴AD⊥平面POB,∵BC∥AD,∴BC⊥平面POB,∵PB 平面POB,
平面POB,
∴BC⊥PB,即∠PBC=90°.
(2)如图,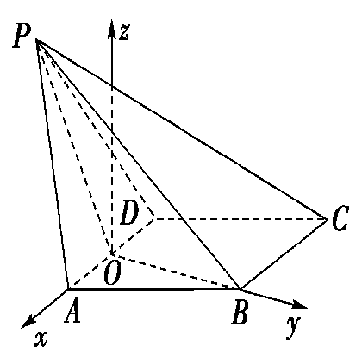
以O为坐标原点,建立空间直角坐标系O-xyz,则A(1,0,0),B(0,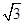 ,0),C(-1,
,0),C(-1,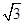 ,0),由PO=BO=
,0),由PO=BO=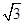 ,PB=3,得∠POB=120°,∴∠POz=30°,∴P(0,-
,PB=3,得∠POB=120°,∴∠POz=30°,∴P(0,- ,
, ),则
),则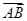 =(-1,
=(-1,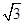 ,0),
,0), =(-1,0,0),
=(-1,0,0),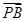 =(0,
=(0,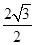 ,-
,- ),设平面PBC的法向量为n=(x,y,z),则
),设平面PBC的法向量为n=(x,y,z),则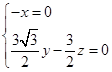 ,取z=
,取z=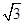 ,则n=(0,1,
,则n=(0,1,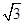 ),
),
设直线AB与平面PBC所成的角为θ,则sinθ=|cos〈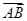 ,n〉|=
,n〉|=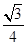 .
.
解析

练习册系列答案
相关题目
 中,平面PAD⊥平面 ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面 ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
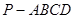 中,底面
中,底面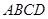 为平行四边形,
为平行四边形,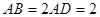 ,
,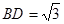 ,
,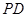 ⊥底面
⊥底面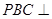 平面
平面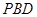 ; ②若二面角
; ②若二面角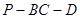 为
为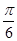 ,求
,求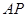 与平面
与平面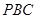 所成角的正弦值.
所成角的正弦值.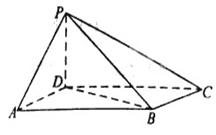
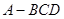 中,面
中,面 面
面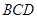 ,
,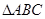 是正三角形,
是正三角形,  ,
,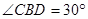 .
.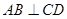 ;
; 与
与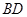 所成角的余弦值.
所成角的余弦值.
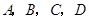 为空间四点.在
为空间四点.在 中,
中, .等边三角形
.等边三角形 以
以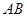 为轴运动.
为轴运动.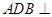 平面
平面 时,求
时,求 ;
;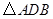 转动时,证明总有
转动时,证明总有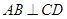 ?
?
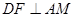 ,垂足为E,若将
,垂足为E,若将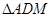 沿AM折起,使点D位于
沿AM折起,使点D位于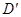 位置,连接
位置,连接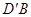 ,
,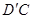 得四棱锥
得四棱锥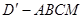 .
. ;(2)若
;(2)若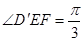 ,直线
,直线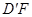 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为 ,求直线
,求直线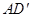 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.
 为圆
为圆 的直径,点
的直径,点 、
、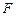 在圆
在圆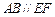 ,矩形
,矩形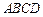 所在的平面和圆
所在的平面和圆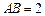 ,
,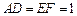 .
.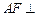 平面
平面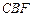 ;
;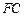 的中点为
的中点为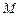 ,求证:
,求证: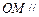 平面
平面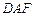 ;
;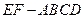 分割成的两个锥体的体积分别为
分割成的两个锥体的体积分别为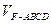 、
、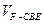 ,求
,求 的值
的值