题目内容
已知定义在 上的三个函数
上的三个函数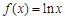 ,
, ,
, ,且
,且 在
在 处取得极值.
处取得极值.


(1)求a的值及函数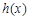 的单调区间.
的单调区间.
(2)求证:当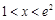 时,恒有
时,恒有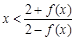 成立.
成立.
 上的三个函数
上的三个函数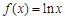 ,
, ,
, ,且
,且 在
在 处取得极值.
处取得极值.


(1)求a的值及函数
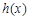 的单调区间.
的单调区间.(2)求证:当
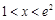 时,恒有
时,恒有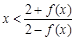 成立.
成立.(1) ,单调递增区间是
,单调递增区间是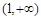 ;单调递减区间是
;单调递减区间是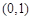 .
.
 ,单调递增区间是
,单调递增区间是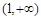 ;单调递减区间是
;单调递减区间是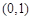 .
.试题分析:解题思路:(1)求导函数,利用
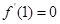 求
求 值,再利用导数求单调区间;(2)作差,构造函数,求最值,即证明不等式恒成立.规律总结:(1)求函数的单调区间的步骤:①求导函数;②解
值,再利用导数求单调区间;(2)作差,构造函数,求最值,即证明不等式恒成立.规律总结:(1)求函数的单调区间的步骤:①求导函数;②解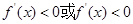 ;③得到区间即为所求单调区间;(2)证明不等式恒成立问题,往往转化为求函数的最值问题.
;③得到区间即为所求单调区间;(2)证明不等式恒成立问题,往往转化为求函数的最值问题.试题解析:(1)
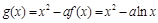 ,
,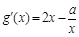 ,
,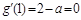 ,
,∴
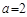 .
.而
 ,
,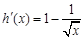 ,令
,令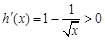 得
得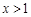 ;令
;令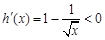 得
得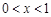 .∴函数
.∴函数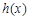 单调递增区间是
单调递增区间是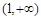 ;单调递减区间是
;单调递减区间是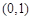 .
.(2)∵
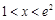 ,∴
,∴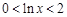 ,∴
,∴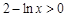 ,
,欲证
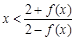 ,只需要证明
,只需要证明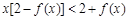 ,即证明
,即证明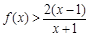 .
.记
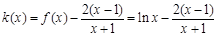 ,∴
,∴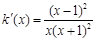 ,
,当
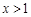 时,
时,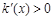 ,∴
,∴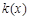 在
在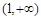 上是增函数,
上是增函数,∴
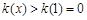 ,∴
,∴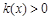 ,即
,即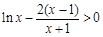 ,
,∴
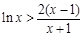 ,故结论成立.
,故结论成立.
练习册系列答案
相关题目
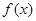 ,当
,当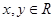 时,恒有
时,恒有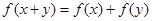 .
.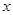 为正实数,
为正实数,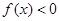 ,并且
,并且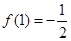 ,试求
,试求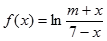 在其定义域上为奇函数.
在其定义域上为奇函数.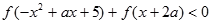 对任意实数
对任意实数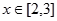 恒成立,求实数
恒成立,求实数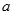 的取值范围.
的取值范围.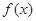 是
是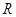 上的增函数,
上的增函数,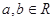 ,且
,且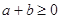 ,求证
,求证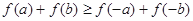
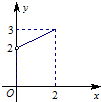
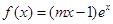 在
在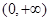 上单调递增,则实数
上单调递增,则实数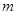 的取值范围是 .
的取值范围是 .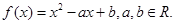
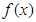 在区间
在区间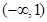 上单调递减,则
上单调递减,则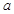 的取值范围 .
的取值范围 .