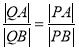题目内容
【题目】[选修4-4：坐标系与参数方程]
在直角坐标系
中，曲线
（
为参数）.以原点
为极点，
轴的正半轴为极轴建立极坐标系，直线
的极坐标方程为
.
（1）求曲线
的普通方程和直线的直角坐标方程；
（2）若曲线与直线交于
两点，点
，求
的值.
【答案】（1）
，
；（2）
【解析】
（1）由曲线
的参数方程，消去参数可直接得到普通方程；由直线的极坐标方程，可直接写出其直角坐标方程；
（2）先由点
在直线
上，得到直线的参数方程为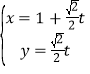
（
为参数），代入曲线的普通方程，结合韦达定理，即可求出结果.
（1）曲线的普通方程为
，
直线的直角坐标方程为
.
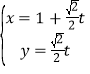（2）点在直线上，直线的参数方程为（为参数），
将直线的参数方程代入曲线的普通方程化简，得
.
设点
，
所对应的参数分别为
，
，则
，
.
所以
.
【题目】某企业生产一种产品，从流水线上随机抽取100件产品，统计其质量指标值并绘制频率分布直方图（如图）：
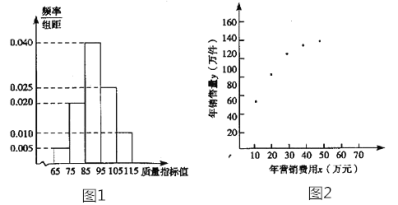
规定产品的质量指标值在
的为劣质品，在
的为优等品，在
的为特优品，销售时劣质品每件亏损1元，优等品每件盈利3元，特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
（1）求每件产品的平均销售利润；
（2）该企业为了解年营销费用
（单位：万元）对年销售量
（单位：万件）的影响，对近5年年营销费用
和年销售量
数据做了初步处理，得到如图的散点图及一些统计量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中
，
，
，
.
根据散点图判断，
可以作为年销售量（万件）关于年营销费用（万元）的回归方程.
①求关于的回归方程；
⑦用所求的回归方程估计该企业应投人多少年营销费，才能使得该企业的年收益的预报值达到最大？（收益=销售利润营销费用，取
）
附：对于一组数据
，
，…，
其回归直线
均斜率和截距的最小二乘估计分别为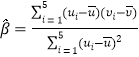
，
.
