题目内容
【题目】已知抛物线C的焦点在y轴上,焦点到准线的距离为2,且对称轴为y轴.
(1)求抛物线C的标准方程;
(2)当抛物线C的焦点为![]() 时,过F作直线交抛物线于,A、B两点,若直线OA,OB(O为坐标原点)分别交直线
时,过F作直线交抛物线于,A、B两点,若直线OA,OB(O为坐标原点)分别交直线![]() 于M、N两点,求
于M、N两点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据抛物线的定义即可求出抛物线方程;
(2)由题意可得抛物线C的方程为![]() ,设
,设![]() ,
,![]() ,直线AB的方程为
,直线AB的方程为![]() ,联立直线与抛物线方程,利用韦达定理求得
,联立直线与抛物线方程,利用韦达定理求得![]() ,联立方程求得点M、N的横坐标,则
,联立方程求得点M、N的横坐标,则![]()
![]() ,利用换元法求最值即可得出答案.
,利用换元法求最值即可得出答案.
解:(1)当焦点在y轴正半轴时,设抛物线C标准方程为![]() ,
,
则![]() ,所以抛物线C的方程为
,所以抛物线C的方程为![]() ,
,
当焦点在y轴负半轴时,设抛物线C标准方程为![]() ,
,
则![]() ,所以抛物线C的方程为
,所以抛物线C的方程为![]() ;
;
(2)依题意,抛物线C的方程为![]() ,设
,设![]() ,
,![]() ,直线AB的方程为
,直线AB的方程为![]() ,
,
由![]() 消去y整理可得:
消去y整理可得:![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
由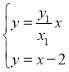 ,解得点M的横坐标为
,解得点M的横坐标为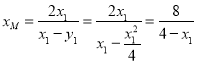 ,
,
同理可得点N的横坐标为![]() ,
,
∴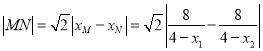
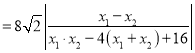
![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,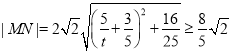 ,
,
此时![]() 即
即![]() ,则
,则![]() ,
,
综上:![]() 的最小值
的最小值![]() .
.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目