函数f(x)=|lnx|的单调递减区间是(0.1]．题目和参考答案——青夏教育精英家教网——

题目内容

17．函数f（x）=|lnx|的单调递减区间是（0，1]．

分析画出函数f（x）=|lnx|的图象，数形结合，可得函数的单调区间．

解答解：函数f（x）=|lnx|=$\left\{\begin{array}{l}-lnx，0＜x≤1\\ lnx，x＞1\end{array}\right.$的图象如下图所示：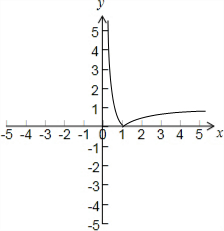

由图可得：函数f（x）=|lnx|的单调递减区间是：（0，1]，
故答案为：（0，1]

点评本题考查的知识点是分段函数的应用，对数函数的图象和性质，难度中档．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

7．已知椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1（m＞n＞0）的离心率为$\frac{1}{2}$，且有一个焦点与抛物线y²=16x的焦点重合，则椭圆的短轴长为8$\sqrt{3}$．

8．若P满足$\frac{{x}^{2}}{4}$+y²=1（y≥0），则$\frac{y-2}{x-4}$的最小值是$\frac{4-\sqrt{7}}{6}$．

5．已知点（3，-2）是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的点，则下列各点中，一定不在该椭圆上的是（　　）

12．求下列各式中x的值：
（1）log₂（log₄x）=0；
（2）log₃（1gx）=1；
（3）log${\;}_{（\sqrt{2}-1）}$$\frac{1}{\sqrt{2}+1}$=x．

2．若函数y=log_a（x+b）（a＞0，a≠1）的图象过两点（-1，0）和（0，1），则a•b=4．

9．已知函数f（x）=-$\frac{\sqrt{3}}{2}$[1+sin（$\frac{3π}{2}$-2x）]+$\frac{1}{2}$cos（$\frac{3π}{2}$+2x），若f（$\frac{α}{2}$）=$\frac{1}{4}$-$\frac{\sqrt{3}}{2}$，α∈（$\frac{π}{3}$，π），求sinα．

6．在Rt△ABC中，CD是斜边上的高线，AC：BC=3：1，则S_△ABC：S_△BCD为（　　）

7．若sinθ+cosθ=$\frac{1}{5}$，θ∈[0，π]，则sinθ=$\frac{4}{5}$，cos2θ=-$\frac{7}{25}$．