题目内容
12.求下列各式中x的值:(1)log2(log4x)=0;
(2)log3(1gx)=1;
(3)log${\;}_{(\sqrt{2}-1)}$$\frac{1}{\sqrt{2}+1}$=x.
分析 根据对数的定义及运算性质,解相应方程,可得答案.
解答 解:(1)∵log2(log4x)=0,
∴log4x=1,
∴x=4;
(2)∵log3(1gx)=1,
∴1gx=3,
∴x=1000;
(3)∵$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}-1$,
∴log${\;}_{(\sqrt{2}-1)}$$\frac{1}{\sqrt{2}+1}$=x=1.
点评 本题考查的知识点是对数方程的解法,正确理解对数的定义,是解答的关键.

练习册系列答案
相关题目
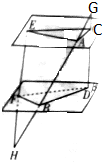 如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.
如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.