题目内容
2.若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,f(x)=$\sqrt{1-x^2}$,则函数H(x)=|xex|-f(x)在区间[-5,1]上的零点个数为6.分析 求出函数m(x)=xex的导函数,由导函数等于0求出x的值,以求出的x的值为分界点把原函数的定义域分段,以表格的形式列出导函数在各区间段内的符号及原函数的增减性,从而得到函数的单调区间及极值点,把极值点的坐标代入原函数求极值.然后判断y=|xex|的极值与单调性,然后推出零点的个数.
解答 解:定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),
∴函数f(x)是偶函数,且函数的图象关于x=1对称.
∵函数m(x)=xex的定义域为R,m′(x)=(xex)′=x′ex+x(ex)′=ex+xex,
令m′(x)=ex+xex=ex(1+x)=0,解得:x=-1.
列表:
| x | (-∞,-1) | -1 | (-1,+∞) |
| m′(x) | - | 0 | + |
| m(x) | ↓ | 极小值 | ↑ |
当x=-1时,函数m(x)=xex的极小值为m(-1)=-$\frac{1}{e}$.
故函数y=|xex|在x=-1时取得极大值为$\frac{1}{e}$,
且y=|xex|在(-∞,-1)上是增函数,在(-1,-∞)上是减函数,
在区间[-5,1]上,故当x<0时,y有5个交点,当x>0时,y有1个交点,共有6个交点,
如图所示:
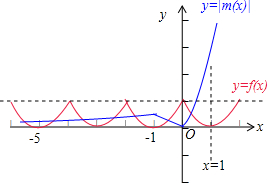
故答案为:6.
点评 本题考查了利用导数研究函数的单调性与极值,在求出导函数等于0的x值后,借助于表格分析能使解题思路更加清晰,此题是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知点F是双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点,点E是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若∠AEB是钝角,则该双曲线的离心率e的取值范围是( )
| A. | $(1+\sqrt{2},+∞)$ | B. | $(1,1+\sqrt{2})$ | C. | (2,+∞) | D. | $(2,1+\sqrt{2})$ |
12.某程序框图如图所示,运行该程序时,输出的S值是( )


| A. | 44 | B. | 70 | C. | 102 | D. | 140 |
19.设坐标原点为O,已知过点(0,$\frac{1}{2}$)的直线交函数y=$\frac{1}{2}$x2的图象于A、B两点,则$\overrightarrow{OA}$•$\overrightarrow{OB}$的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
