题目内容
2.设a>1,函数f(x)=(1+x2)ex-a.(1)求f(x)的单调区间;
(2)证明f(x)在(-∞,+∞)上仅有一个零点;
(3)若曲线y=f(x)在点P处的切线与x轴平行,且在点M(m,n)处的切线与直线OP平行,(O是坐标原点),证明:m≤$\root{3}{a-\frac{2}{e}}$-1.
分析 (1)利用f′(x)>0,求出函数单调增区间.
(2)证明只有1个零点,需要说明两个方面:①函数单调;②函数有零点.
(3)利用导数的最值求解方法证明,思路较为复杂.
解答 解:(1)f′(x)=ex(x2+2x+1)=ex(x+1)2,
∴f′(x)≥0,
∴f(x)=(1+x2)ex-a在(-∞,+∞)上为增函数.
(2)证明:∵f(0)=1-a,a>1,
∴1-a<0,即f(0)<0,
∵f($\sqrt{a}$)=(1+a)${e}^{\sqrt{a}}$-a=${e}^{\sqrt{a}}$+a(${e}^{\sqrt{a}}$-1),a>1,
∴${e}^{\sqrt{a}}$>1,${e}^{\sqrt{a}}$-1>0,即f($\sqrt{a}$)>0,
且由(1)问知函数在(-∞,+∞)上为增函数,
∴f(x)在(-∞,+∞)上有且只有一个零点.
(3)证明:f′(x)=ex(x+1)2,
设点P(x0,y0)则)f'(x)=ex0(x0+1)2,
∵y=f(x)在点P处的切线与x轴平行,
∴f′(x0)=0,即:ex0(x0+1)2=0,
∴x0=-1,
将x0=-1代入y=f(x)得y0=$\frac{2}{e}-a$.
∴${k}_{op}=\frac{\frac{2}{e}-a}{-1}=a-\frac{2}{e}$,
∴$f'(m)={e}^{m}(m+1)^{2}=a-\frac{2}{e}$,
要证m≤$\root{3}{a-\frac{2}{e}}$-1,即证(m+1)3≤a-$\frac{2}{e}$,
需要证(m+1)3≤em(m+1)2,
即证m+1≤em,
因此构造函数g(m)=em-(m+1),
则g′(m)=em-1,由g′(m)=0得m=0.
当m∈(0,+∞)时,g′(m)>0,
当m∈(-∞,0)时,g′(m)<0,
∴g(m)的最小值为g(0)=0,
∴g(m)=em-(m+1)≥0,
∴em≥m+1,
∴em(m+1)2≥(m+1)3,
即:$a-\frac{2}{e}≥(m+1)^{3}$,
∴m≤$\root{3}{a-\frac{2}{e}}-1$.
点评 本题考查了导数在函数单调性和最值上的应用,属于综合应用,在高考中属于压轴题目,有较大难度.


| A. | 1+$\sqrt{3}$ | B. | 1+2$\sqrt{2}$ | C. | 2+$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
| A. | 至多等于3 | B. | 至多等于4 | C. | 等于5 | D. | 大于5 |
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
| A. | (2,3) | B. | (2,4] | C. | (2,3)∪(3,4] | D. | (-1,3)∪(3,6] |
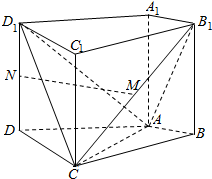 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.