题目内容
13.一个四面体的三视图如图所示,则该四面体的表面积是( )
| A. | 1+$\sqrt{3}$ | B. | 1+2$\sqrt{2}$ | C. | 2+$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
分析 判断得出三棱锥O-ABC,OE⊥底面ABC,EA=ED=1,OE=1,AB=BC=$\sqrt{2}$,AB⊥BC,
可判断;△OAB≌△OBC的直角三角形,
运用面积求解即可.
解答 解:∵
∴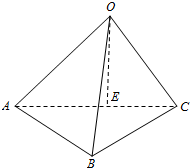
三棱锥O-ABC,OE⊥底面ABC,EA=ED=1,OE=1,AB=BC=$\sqrt{2}$
∴AB⊥BC,
∴可判断;△OAB≌△OBC的直角三角形,
S△OAC=S△ABC=$\frac{1}{2}×2×1$=1,
S△OAB=S△OBC=$\frac{\sqrt{3}}{4}$×$(\sqrt{2})$2=$\sqrt{3}$
该四面体的表面积:2$+\sqrt{3}$,
故选:C.
点评 本题考查了三棱锥的三视图的运用,关键是恢复几何体的直观图,考查了学生的空间思维能力.

练习册系列答案
相关题目
1.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
| A. | 36π | B. | 64π | C. | 144π | D. | 256π |
 如图,三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.
如图,三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.