题目内容
10.已知函数f(x)=ax3+x+1的图象在点(1,f(1))处的切线过点(2,7),则a=1.分析 求出函数的导数,利用切线的方程经过的点求解即可.
解答 解:函数f(x)=ax3+x+1的导数为:f′(x)=3ax2+1,f′(1)=3a+1,而f(1)=a+2,
切线方程为:y-a-2=(3a+1)(x-1),因为切线方程经过(2,7),
所以7-a-2=(3a+1)(2-1),
解得a=1.
故答案为:1.
点评 本题考查函数的导数的应用,切线方程的求法,考查计算能力.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
1.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
| A. | 36π | B. | 64π | C. | 144π | D. | 256π |
19.设命题p:?n∈N,n2>2n,则¬p为( )
| A. | ?n∈N,n2>2n | B. | ?n∈N,n2≤2n | C. | ?n∈N,n2≤2n | D. | ?n∈N,n2=2n |
20.已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩∁UB=( )
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |
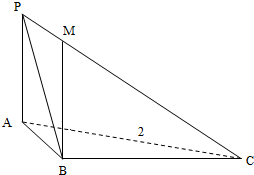 如图,三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.
如图,三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB=1,AC=2,∠BAC=60°.