题目内容
已知数列 满足
满足 ,
, .
.
(1)求证:数列 为等差数列;
为等差数列;
(2)求数列 的通项公式;
的通项公式;
(3)当 时,若
时,若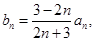 求
求 的值.
的值.
 满足
满足 ,
, .
.(1)求证:数列
 为等差数列;
为等差数列;(2)求数列
 的通项公式;
的通项公式;(3)当
 时,若
时,若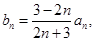 求
求 的值.
的值.(1)详见解析;(2)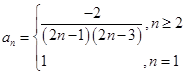 ;(3)
;(3)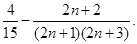
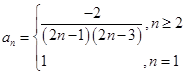 ;(3)
;(3)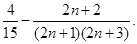
(1)证明数列 为等差数列,实质就是证明:当
为等差数列,实质就是证明:当 时,
时,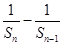 为一个常数. 由当
为一个常数. 由当 时,
时,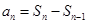 ,可将
,可将 化为
化为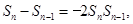 ,整理得
,整理得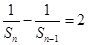 ;(2)由(1)可先求出
;(2)由(1)可先求出 通项:
通项: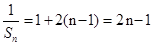 ,所以
,所以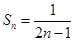 ,再由当
,再由当 时,
时,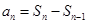 求出
求出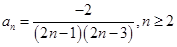 ,由于当
,由于当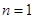 时,
时,
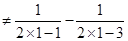 ,所以
,所以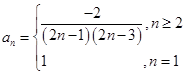 ;(3)当
;(3)当 时,
时,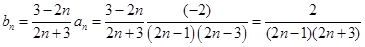 ,这是一个分式数列,其求和通常利用裂项相消法,即
,这是一个分式数列,其求和通常利用裂项相消法,即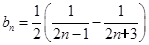 ,因此
,因此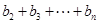
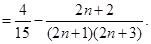
试题分析:
试题解析:(1)当 时,
时,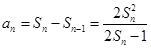 ,整理得
,整理得
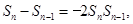 故
故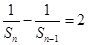 ,且
,且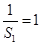 , 2分
, 2分
所以 为以1为首项,2为公差的等差数列. 4分
为以1为首项,2为公差的等差数列. 4分
(2)由(1)可知,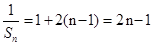 ,所以
,所以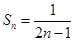
方法1:
当 时,
时,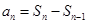 =
=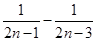 , 6分
, 6分
当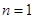 时,
时,
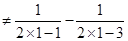
则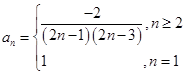 8分
8分
方法2:由已知当 时,
时,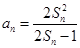 ,将
,将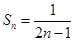 代入,可得
代入,可得
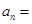
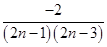 6分
6分
经验证,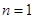 时,不符
时,不符
综上,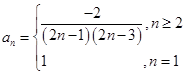 8分
8分
(III)当 时,
时,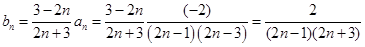 ,
,
所以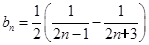 10分
10分
则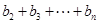
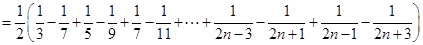
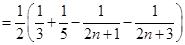
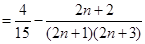 (
( )12分
)12分
 为等差数列,实质就是证明:当
为等差数列,实质就是证明:当 时,
时,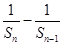 为一个常数. 由当
为一个常数. 由当 时,
时,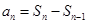 ,可将
,可将 化为
化为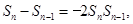 ,整理得
,整理得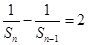 ;(2)由(1)可先求出
;(2)由(1)可先求出 通项:
通项: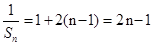 ,所以
,所以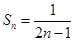 ,再由当
,再由当 时,
时,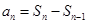 求出
求出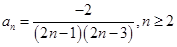 ,由于当
,由于当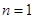 时,
时,
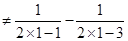 ,所以
,所以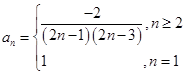 ;(3)当
;(3)当 时,
时,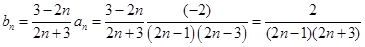 ,这是一个分式数列,其求和通常利用裂项相消法,即
,这是一个分式数列,其求和通常利用裂项相消法,即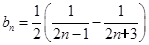 ,因此
,因此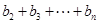
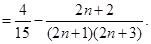
试题分析:
试题解析:(1)当
 时,
时,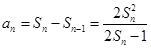 ,整理得
,整理得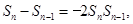 故
故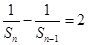 ,且
,且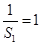 , 2分
, 2分所以
 为以1为首项,2为公差的等差数列. 4分
为以1为首项,2为公差的等差数列. 4分(2)由(1)可知,
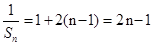 ,所以
,所以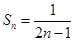
方法1:
当
 时,
时,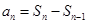 =
=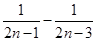 , 6分
, 6分当
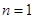 时,
时,
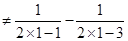
则
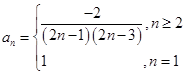 8分
8分方法2:由已知当
 时,
时,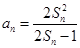 ,将
,将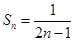 代入,可得
代入,可得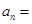
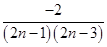 6分
6分经验证,
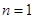 时,不符
时,不符综上,
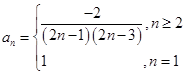 8分
8分(III)当
 时,
时,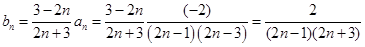 ,
,所以
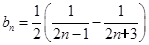 10分
10分则
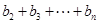
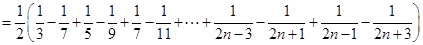
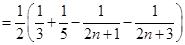
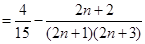 (
( )12分
)12分
练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
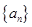 是首项为
是首项为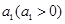 ,公差为
,公差为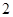 的等差数列,其前
的等差数列,其前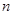 项和为
项和为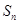 ,且
,且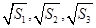 成等差数列.
成等差数列.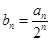 的前
的前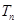 ,求
,求 中,
中, ,且
,且 成等比数列.
成等比数列. ,试比较
,试比较 与
与 的大小,并说明理由.
的大小,并说明理由.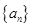 为等差数列,且
为等差数列,且 ,
,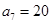 .设数列
.设数列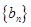 的前
的前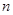 项和为
项和为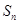 ,且
,且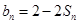 .
.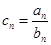 ,
,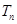 为数列
为数列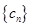 的前
的前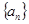 满足
满足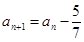 ,且
,且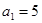 ,设
,设 项和为
项和为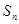 ,则使得
,则使得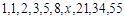 中,
中,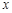 等于( )
等于( )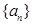 满足
满足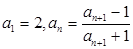 ,其前
,其前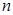 项积为
项积为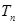 ,则
,则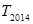 =( )
=( )



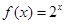 ,等差数列
,等差数列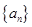 的公差为
的公差为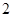 ,a1=1,则
,a1=1,则