题目内容
【题目】如图，在四棱锥
中，平面
平面
，底面为平行四边形，
，
.
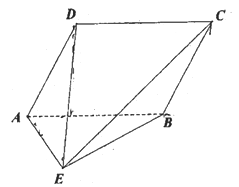
（1）求
的长；
（2）求二面角
的余弦值.
【答案】（1）
之长为
；（2）二面角
的余弦值为
.
【解析】试题分析：（1）如图，过
点作
于垂足
．可得
平面
．
过点在平面内作
，交
于点
，
建立以为坐标原点，
为
轴，
为
轴，
为
轴的空间直角坐标系，
可得
，
，
，
，
，即可所求
之长．
（2）求出平面
的法向量
，，平面
的法向量
，
，即可得二面角
的平面角的余弦值．
试题解析：（Ⅰ）如图，过点作于垂足．
∵平面
平面，
∴平面．
过点在平面内作，交于点，
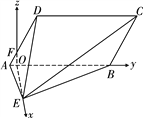
建立以为坐标原点，为轴，为轴，为轴的空间直角坐标系，
∵
，
，
，
，
∴
，
∴，，，，
，
∴
.
（Ⅱ）设平面的法向量，
而
，
由
及
可得，
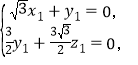可取
，
设平面的法向量，
，
由
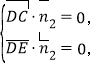得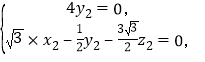
可取
，
∴
，
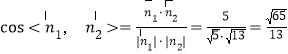∴二面角的余弦值为
.
练习册系列答案
相关题目
【题目】从某工厂的一个车间抽取某种产品
件，产品尺寸（单位：
）落在各个小组的频数分布如下表：
数据分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
（1）根据频数分布表，求该产品尺寸落在
的概率；
（2）求这件产品尺寸的样本平均数
；（同一组中的数据用该组区间的中点值作代表）
（3）根据频数分布对应的直方图，可以认为这种产品尺寸
服从正态分布
，其中
近似为样本平均值，
近似为样本方差
，经过计算得
，利用该正态分布，求
.
附：①若随机变量服从正态分布，则
，
；②
.
