题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)设函数![]() ,
, ![]() .若函数
.若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() ,
, ![]() 的定义域都是
的定义域都是![]() ,对于函数
,对于函数![]() 的图象上的任意一点
的图象上的任意一点![]() ,在函数
,在函数![]() 的图象上都存在一点
的图象上都存在一点![]() ,使得
,使得![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数, ![]() 为坐标原点.求
为坐标原点.求![]() 的取值范围.
的取值范围.
【答案】(1)(2)
【解析】试题分析:求函数的单调区间可利用求导完成,求函数的最值可通过求导研究函数的单调性求出极值,并与区间端点函数值比较得出最值;解决![]() 问题,先求出
问题,先求出![]() 斜率的取值范围,根据垂直关系得出
斜率的取值范围,根据垂直关系得出![]() 斜率的取值范围,转化为恒成立问题,借助恒成立思想解题.
斜率的取值范围,转化为恒成立问题,借助恒成立思想解题.
试题解析:
(1)当![]() 时,
时, ![]() ,
, ![]() .
.
因为![]() 在
在![]() 上单调增,且
上单调增,且![]() ,
,
所以当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]() 的单调增区间是
的单调增区间是![]() .
.
(2)![]() ,则
,则![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在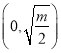 上单调减;
上单调减;
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在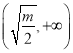 上单调增.
上单调增.
所以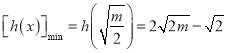 .
.
①当![]() ,即
,即![]() 时,
时,
函数![]() 的最小值
的最小值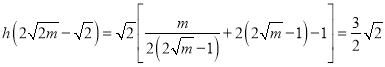 ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍),所以
(舍),所以![]() ;
;
②当![]() ,即
,即![]() 时,
时,
函数![]() 的最小值
的最小值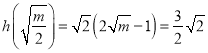 ,解得
,解得![]() (舍).
(舍).
综上所述, ![]() 的值为
的值为![]() .
.
(3)由题意知, ![]() ,
, ![]() .
.
考虑函数![]() ,因为
,因为![]() 在
在![]() 上恒成立,
上恒成立,
所以函数![]() 在
在![]() 上单调增,故
上单调增,故![]() .
.
所以![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
设![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调减,所以
上单调减,所以![]() .
.
设![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调增,所以
上单调增,所以![]() .
.
综上所述, ![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
车间 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.