题目内容
(本小题满分14分)
已知函数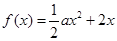 ,
,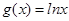 .
.
(1)如果函数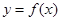 在
在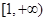 上是单调增函数,求
上是单调增函数,求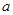 的取值范围;
的取值范围;
(2)是否存在实数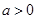 ,使得方程
,使得方程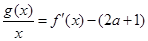 在区间
在区间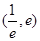 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出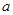 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(1)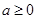 (2)(
(2)( )
)
【解析】
试题分析:(1)当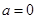 时,
时, 在
在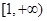 上是单调增函数,符合题意.
……1分
上是单调增函数,符合题意.
……1分
当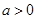 时,
时,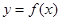 的对称轴方程为
的对称轴方程为 ,
,
由于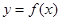 在
在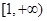 上是单调增函数,
上是单调增函数,
所以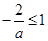 ,解得
,解得 或
或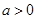 ,
,
所以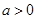 . ……3分
. ……3分
当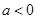 时,不符合题意.
时,不符合题意.
综上, 的取值范围是
的取值范围是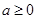 . ……4分
. ……4分
(2)把方程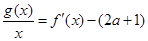 整理为
整理为 ,
,
即为方程 . ……5分
. ……5分
设
 ,
,
原方程在区间(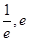 )内有且只有两个不相等的实数根,
)内有且只有两个不相等的实数根,
即为函数 在区间(
在区间(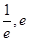 )内有且只有两个零点.
……6分
)内有且只有两个零点.
……6分
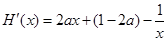
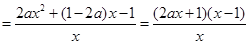 ,
……7分
,
……7分
令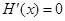 ,因为
,因为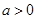 ,解得
,解得 或
或 (舍),
……8分
(舍),
……8分
当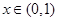 时,
时,  ,
,  是减函数;
是减函数;
当 时,
时, 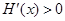 ,
, 是增函数.
……10分
是增函数.
……10分
 在(
在(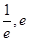 )内有且只有两个不相等的零点, 只需
)内有且只有两个不相等的零点, 只需 ……13分
……13分
即 ∴
∴ ,
,
解得 , 所以
, 所以 的取值范围是(
的取值范围是( ) . ……14分
) . ……14分
考点:本小题主要考查二次函数的单调性和利用导数解决函数的单调性、最值问题,考查学生对导数的工具性的应用能力和分类讨论思想和数形结合思想的应用.
点评:研究高次函数的单调性一般用导数,前提是合理构造函数并正确求导,而不论用什么方法考查函数的性质,都不能忘记函数的定义域.

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)