题目内容
（2013•宁波二模）已知平面α、β、γ、和直线l，m，且l⊥m，α⊥γ，α∩γ=m，γ∩β=l；给出下列四个结论：①β⊥γ ②l⊥α③m⊥β；④α⊥β．其中正确的是（ ）
分析：根据面面垂直判定定理进行证明可知②正确，根据线面垂直的性质定理可知④正确，对于①③可举例说明即可．
解答：解：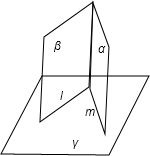
平面α、β、γ，直线l、m，且l⊥m，α⊥γ，α∩γ=m，γ∩β=l，
②∵α⊥γ，设直线n?α，且n⊥γ，∴n⊥l 又∵m⊥l，且m，n相交
∴l垂直于m，n所在平面，即l⊥α，又∵l?β，∴β⊥α，（线面垂直的性质定理），故④成立，
①③不成立如图所示，
故选B．
平面α、β、γ，直线l、m，且l⊥m，α⊥γ，α∩γ=m，γ∩β=l，②∵α⊥γ，设直线n?α，且n⊥γ，∴n⊥l 又∵m⊥l，且m，n相交
∴l垂直于m，n所在平面，即l⊥α，又∵l?β，∴β⊥α，（线面垂直的性质定理），故④成立，
①③不成立如图所示，
故选B．
点评：本题考查空间中直线与平面之间的位置关系，考查对基础知识的综合应用能力和基本定理的掌握能力，属基础题．
练习册系列答案
习题精选系列答案
相关题目
（2013•宁波二模）如图是某学校抽取的n个学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率之比为1：2：3，第3个小组的频数为18，则的值n是