题目内容
【题目】如图,在长方体A1B1C1D1﹣ABCD中,AD=CD=4,AD1=5,M是线段B1D1的中点. 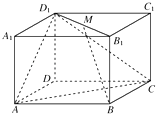
(1)求证:BM∥平面D1AC;
(2)求直线DD1与平面D1AC所成角的正弦值.
【答案】
(1)解:在长方体A1B1C1D1﹣ABCD中,
∵AD=4,AD1=5,∴DD1= ![]() =3,
=3,
以D为原点,DA,DA,DD1分别为xyz轴建立空间直角坐标系D﹣xyz,
根据题意得A(4,0,0),B(4,4,0),C(0,4,0),D(0,0,0),
B1(4,4,3),D1(0,0,3),线段B1D1的中点为M(2,2,3),线段AC的中点为N(2,2,0).
∴ ![]() =(﹣2,﹣2,3),
=(﹣2,﹣2,3), ![]() =(﹣2,﹣2,3).∴
=(﹣2,﹣2,3).∴ ![]() ∥
∥ ![]() ,∴BM∥ND1.
,∴BM∥ND1.
∵BM平面D1AC,ND1平面D1AC,∴BM∥平面D1AC
(2)解:∵ ![]() =(0,0,3),
=(0,0,3), ![]() =(﹣4,4,0),
=(﹣4,4,0), ![]() =(﹣4,0,3),
=(﹣4,0,3),
设平面D1AC的法向量为 ![]() =(x,y,z),
=(x,y,z),
根据已知得 ![]() =﹣4x+4y=0,且
=﹣4x+4y=0,且 ![]() =﹣4x+3z=0,
=﹣4x+3z=0,
取x=1,可得y=1,z= ![]() ,∴
,∴ ![]() =(1,1,
=(1,1, ![]() )是平面D1AC的一个法向量,
)是平面D1AC的一个法向量,
∴cos< ![]() ,
, ![]() >=
>= 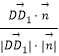 =
= ![]() ,
,
∴直线DD1与平面D1AC所成角的正弦值等于 ![]()
【解析】(1)以D为原点,DA,DA,DD1分别为xyz轴建立空间直角坐标系D﹣xyz,由坐标法可证 ![]() ∥
∥ ![]() ,进而可得BM∥ND1 . 由线面平行的判定定理可得;(2)设平面D1AC的法向量为
,进而可得BM∥ND1 . 由线面平行的判定定理可得;(2)设平面D1AC的法向量为 ![]() =(x,y,z),根据
=(x,y,z),根据 ![]() =﹣4x+4y=0,且
=﹣4x+4y=0,且 ![]() =﹣4x+3z=0,可求,进而可得cos<
=﹣4x+3z=0,可求,进而可得cos< ![]() ,
, ![]() >,即得所求.
>,即得所求.
【考点精析】掌握直线与平面平行的判定和空间角的异面直线所成的角是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则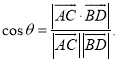 .
.

【题目】某工厂为了对新研究的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销售y件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]() =﹣20.
=﹣20.
(2)预计在今后的销售中,销售与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价定为多少元?