题目内容
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系中,已知直线![]() 过点
过点![]() ,倾斜角
,倾斜角![]() ,再以原点为极点,
,再以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)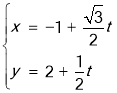 (
(![]() 为参数),x2+y2=9(2)4
为参数),x2+y2=9(2)4
【解析】
试题分析:(1)利用参数方程几何意义得![]() ,即得直线
,即得直线![]() 的参数方程,根据
的参数方程,根据![]() 将极坐标方程化为直角坐标方程x2+y2=9(2)联立直线参数方程与圆方程得关于参数t的方程:
将极坐标方程化为直角坐标方程x2+y2=9(2)联立直线参数方程与圆方程得关于参数t的方程:![]() ,根据直线参数几何意义得|PM||PN|=|t1t2|=4.
,根据直线参数几何意义得|PM||PN|=|t1t2|=4.
试题解析:(1)直线![]() 的参数方程:
的参数方程: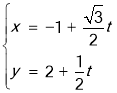 (
(![]() 为参数),
为参数),
曲线C的极坐标方程为ρ=3,可得曲线C的直角坐标方程x2+y2=9.
(2)将直线的参数方程代入x2+y2=9,得![]() ,
,
设上述方程的两根为t1,t2,则t1t2=﹣4.
由直线参数方程中参数t的几何意义可得|PM||PN|=|t1t2|=4.

练习册系列答案
相关题目
【题目】为了参加市高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出![]() 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
班级 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
人数 | 12 | 6 | 9 | 9 |
(1)现采取分层抽样的方法从这四个班中抽取运动员,求应分别从这四个班抽出的队员人数;
(2)该中学篮球队奋力拼搏,获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.