题目内容
6.已知P是△ABC所在平面内一点,4$\overrightarrow{PB}$+5$\overrightarrow{PC}$+3$\overrightarrow{PA}$=$\overrightarrow{0}$,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{12}$ | D. | $\frac{1}{2}$ |
分析 根据4$\overrightarrow{PB}$+5$\overrightarrow{PC}$+3$\overrightarrow{PA}$=$\overrightarrow{0}$,计算△PBC的面积,代入几何概型概率公式,可得答案.
解答 解:令$\overrightarrow{PD}$=4$\overrightarrow{PB}$,$\overrightarrow{PE}$=5$\overrightarrow{PC}$,$\overrightarrow{PF}$=3$\overrightarrow{PA}$,
则∵4$\overrightarrow{PB}$+5$\overrightarrow{PC}$+3$\overrightarrow{PA}$=$\overrightarrow{0}$,
∴$\overrightarrow{PD}$+$\overrightarrow{PE}$+$\overrightarrow{PF}$=$\overrightarrow{0}$,
即P为△DEF的重心,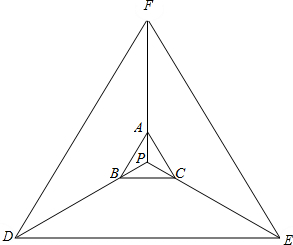
此时△PDE,△PEF,△PDF的面积相等,
则△PDE的面积是△PBC的20倍,
△PEF的面积是△PAC的15倍,
△PDF的面积是△PAB的12倍,
故△ABC的面积是△PBC的4倍,
故将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是$\frac{1}{4}$,
故选:A.
点评 本题考查的知识点是几何概型概率计算公式,计算出满足条件和所有基本事件对应的几何量,是解答的关键,难度中档.

练习册系列答案
相关题目
11.在等比数列{an}中,a2=$\frac{1}{4}$,q=4,则a4与a8的等比中项是( )
| A. | 64 | B. | ±64 | C. | $\frac{1}{64}$ | D. | $±\frac{1}{64}$ |
14.某教辅集团进年要研究出版多种一轮用书,其中有A,B两种已经投入使用,经一学年使用过后,教辅团队为了调查书的质量与社会反响,特地选择某校高三的4个班进行调查,从各班抽取的样本人数如表:
(1)从10人中随机抽取2人,求这2人恰好来自同一班级的概率;
(2)从中这10名学生中,指定甲、乙、丙三人为代表,已知他们每人选择一种图书,其中选择A,B两种图书学习的概率分别是$\frac{1}{3}$,$\frac{2}{3}$,且他们选择A,B任一种图书都是相互独立的,设这三名学生中选择B的人数为ξ,求ξ的分布列和数学期望.
| 班级 | 一 | 二 | 三 | 四 |
| 人数 | 1 | 2 | 3 | 4 |
(2)从中这10名学生中,指定甲、乙、丙三人为代表,已知他们每人选择一种图书,其中选择A,B两种图书学习的概率分别是$\frac{1}{3}$,$\frac{2}{3}$,且他们选择A,B任一种图书都是相互独立的,设这三名学生中选择B的人数为ξ,求ξ的分布列和数学期望.
1.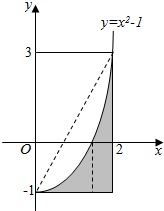 如图,设区域D={(x,y)|0≤x≤2,-1≤y≤3},在区域D内任取一点,则此点落在阴影区域M={(x,y)|0≤x≤2,-1≤y≤x2-1}内的概率为( )
如图,设区域D={(x,y)|0≤x≤2,-1≤y≤3},在区域D内任取一点,则此点落在阴影区域M={(x,y)|0≤x≤2,-1≤y≤x2-1}内的概率为( )
 如图,设区域D={(x,y)|0≤x≤2,-1≤y≤3},在区域D内任取一点,则此点落在阴影区域M={(x,y)|0≤x≤2,-1≤y≤x2-1}内的概率为( )
如图,设区域D={(x,y)|0≤x≤2,-1≤y≤3},在区域D内任取一点,则此点落在阴影区域M={(x,y)|0≤x≤2,-1≤y≤x2-1}内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{7}$ |
16.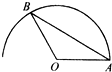 如图所示,OA=1,在以O为圆心,OA为半径的半圆弧长任取一点B,则使△AOB的面积大于等于$\frac{1}{4}$的概率为( )
如图所示,OA=1,在以O为圆心,OA为半径的半圆弧长任取一点B,则使△AOB的面积大于等于$\frac{1}{4}$的概率为( )
 如图所示,OA=1,在以O为圆心,OA为半径的半圆弧长任取一点B,则使△AOB的面积大于等于$\frac{1}{4}$的概率为( )
如图所示,OA=1,在以O为圆心,OA为半径的半圆弧长任取一点B,则使△AOB的面积大于等于$\frac{1}{4}$的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |