题目内容
11.由曲线y=$\sqrt{x}$、直线y=-x+2及x轴所围成的图形的面积为( )| A. | $\frac{10}{3}$ | B. | 4 | C. | $\frac{7}{6}$ | D. | 6 |
分析 利用定积分知识求解该区域面积是解决本题的关键,要确定出曲线y=$\sqrt{x}$、直线y=-x+2的交点,确定出积分区间和被积函数,利用导数和积分的关系完成本题的求解.
解答 解:联立方程$\left\{\begin{array}{l}{y=\sqrt{x}}\\{y=-x+2}\end{array}\right.$得到两曲线的交点(1,1),
因此曲线线y=$\sqrt{x}$、直线y=-x+2及x轴所围成的图形的面积为:
S=${∫}_{0}^{1}\sqrt{x}dx$+$\frac{1}{2}×1×1$=$\frac{2}{3}{x}^{\frac{3}{2}}{|}_{0}^{1}$+$\frac{1}{2}$=$\frac{7}{6}$.
故选:C.
点评 本题考查曲边图形面积的计算问题,考查学生分析问题解决问题的能力和意识,考查学生的转化与化归能力和运算能力,考查学生对定积分与导数的联系的认识,求定积分关键要找准被积函数的原函数,属于定积分的简单应用问题.

练习册系列答案
相关题目
2.已知A={-2,2010,x2-1},B={0,2010,x2-3x},且A=B,则x的值为( )
| A. | 1 | B. | 0 | C. | -1 | D. | -1,1 |
19.已知函数f(x)=2x+log2x,g(x)=2xlog2x+1,h(x)=2xlog2x-1的零点分别为a,b,c,则 a,b,c的大小关系为( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c |
16.满足不等式组$\left\{{\begin{array}{l}{3x-2y-2>0}\\{x+4y+4>0}\\{2x+y-6<0}\end{array}}\right.$任意一点(x,y)都使不等式x+y+m≥0恒成立,则实数m的取值范围为( )
| A. | (1,+∞) | B. | [1,+∞) | C. | [-2,+∞) | D. | (-∞,4] |
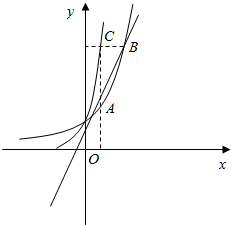 如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).
如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).