题目内容
10.已知△ABC中,cosB=$\frac{4\sqrt{3}}{7}$,BC=3,$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{DC}$,∠ADC=$\frac{π}{3}$.(1)求AD的长;
(2)求△ABC的面积.
分析 (1)由题意画出图象求出BD的值,由两角差的正弦公式求出sin∠BAD,由正弦定理求出AD的值;
(2)过A做AE⊥BC,垂足为E,在RT△ADE中由正弦函数求出AE,再求出△ABC的面积.
解答 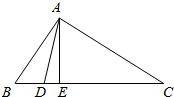 解:(1)由题意画出图象:
解:(1)由题意画出图象:
由BC=3,$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{DC}$得,BD=1,DC=2,
又cosB=$\frac{4\sqrt{3}}{7}$,在△ABD中,sin∠BAD=sin($\frac{π}{3}-B$)
=sin$\frac{π}{3}$cosB-cos$\frac{π}{3}$sinB=$\frac{\sqrt{3}}{2}×\frac{4\sqrt{3}}{7}-\frac{1}{2}•\sqrt{1-(\frac{4\sqrt{3}}{7})^{2}}$
=$\frac{12}{14}-\frac{1}{14}$=$\frac{11}{14}$,
由正弦定理得$\frac{BD}{sin∠BAD}=\frac{AD}{sinB}$,则$\frac{1}{\frac{11}{14}}=\frac{AD}{\frac{1}{7}}$,解得AD=$\frac{2}{11}$;
(2)过A做AE⊥BC,垂足为E,
在RT△ADE中,AE=ADsin$\frac{π}{3}$=$\frac{2}{11}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{11}$,
所以△ABC的面积S=$\frac{1}{2}•BC•AE$=$\frac{1}{2}×3×\frac{\sqrt{3}}{11}$=$\frac{3\sqrt{3}}{22}$.
点评 本题考查正弦定理,三角形的面积公式,以及两角差的正弦公式的应用,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $±\frac{3}{5}$ | D. | $-\frac{4}{5}$ |
| A. | x2+y2+3x+6y=0 | B. | x2+y2-3x+6y=0 | C. | x2+y2+3x-6y=0 | D. | x2+y2-3x-6y=0 |
| A. | |a|>$\sqrt{2}$ | B. | $\sqrt{2}$<|a|<$\sqrt{3}$ | C. | |a|>$\sqrt{3}$ | D. | |a|<3 |
| A. | R | B. | Φ | C. | {0} | D. | {x|x≠0} |