题目内容
定义在R上的函数f（x）满足：f（x+y）=f（x）f（y），且当x＞0时，f（x）＞1．数列{an}满足an=1-3k，f（an+1）=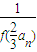
．（1）求f（0）的值，并证明f（x）是定义域上的增函数：
（2）求数列{an}的通项公式；
（3）设0＜a＜bnSn为数列{an}的前n项和，是否存在实数k，使得对任意正整数n，都有a＜Sn＜b？若存在，求出k的取值范围，若不存在，请说明理由．
【答案】分析：（1）利用f（x+y）=f（x）f（y），进行赋值，令x=1，y=0，可得f（0）=1，再证明x∈R时，f（x）＞0，利用函数单调性的定义证明f（x）是定义域上的增函数的关键是f（x1）-f（x2）=f[（x1-x2）+x2]-f（x2）；
（2）f（an+1）=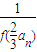
=
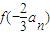，由函数的单调性知，an+1=
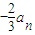，由此可得数列的通项；
（3）求出Sn=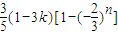
，要使a＜Sn＜b对任意正整数n成立，即
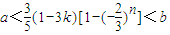，从而可得
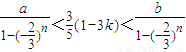，进一步可得
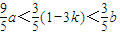，由此可得k的取值范围．
解答：解：（1）令x=1，y=0可得f（1）=f（1）f（0）
∵f（1）＞1，∴f（0）=1
当x＜0时，f（x-x）=f（0）=f（x）f（-x）=1
-x＞0，f（-x）＞1，∴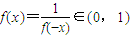
∴x∈R时，f（x）＞0
任取x1＜x2，则f（x1）-f（x2）=f[（x1-x2）+x2]-f（x2）=f（x1-x2）f（x2）-f（x2）=f（x2）[f（x1-x2）-1]
∵x1＜x2，∴x1-x2＜0
∵x＜0时，f（x）＜1，∴f（x1-x2）-1＜0
∴f（x1）-f（x2）＜0，∴f（x1）＜f（x2）
∴f（x）是定义域上的增函数；
（2）f（an+1）=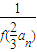
=
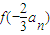，由函数的单调性知，an+1=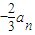
∵a1=1-3k，∴当k=
时，an=0
当k≠
时，an=（1-3k）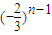
；
（3）由（2）知，当k=
时，an=0，Sn=0，不满足条件；
当k≠
时，an=（1-3k）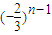
，Sn=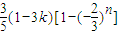
要使a＜Sn＜b对任意正整数n成立，即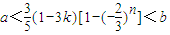
∴
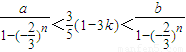
令g（n）=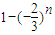
当n为正奇数时，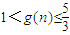
；当n为正偶数时，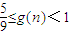
∴g（n）的最大值为g（1）=
，最小值为g（2）=
∴
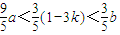
∴3a＜1-3k＜b
∴
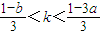
∴当a＜b≤3a时，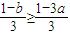
，不存在实数k满足条件；
当b＞3a时，
，存在实数k，使得对任意正整数n，都有a＜Sn＜b，且k的取值范围为（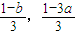
）．
点评：本题考查函数的单调性，考查函数的性质，考查赋值法的而运用，考查存在性问题的探究，属于中档题．
（2）f（an+1）=
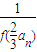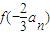=，由函数的单调性知，an+1=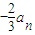，由此可得数列的通项；（3）求出Sn=
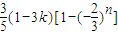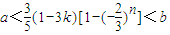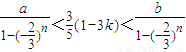，要使a＜Sn＜b对任意正整数n成立，即，从而可得，进一步可得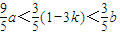，由此可得k的取值范围．解答：解：（1）令x=1，y=0可得f（1）=f（1）f（0）
∵f（1）＞1，∴f（0）=1
当x＜0时，f（x-x）=f（0）=f（x）f（-x）=1
-x＞0，f（-x）＞1，∴
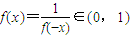
∴x∈R时，f（x）＞0
任取x1＜x2，则f（x1）-f（x2）=f[（x1-x2）+x2]-f（x2）=f（x1-x2）f（x2）-f（x2）=f（x2）[f（x1-x2）-1]
∵x1＜x2，∴x1-x2＜0
∵x＜0时，f（x）＜1，∴f（x1-x2）-1＜0
∴f（x1）-f（x2）＜0，∴f（x1）＜f（x2）
∴f（x）是定义域上的增函数；
（2）f（an+1）=
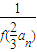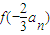=，由函数的单调性知，an+1=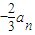∵a1=1-3k，∴当k=
时，an=0当k≠
时，an=（1-3k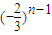）；（3）由（2）知，当k=
时，an=0，Sn=0，不满足条件；当k≠
时，an=（1-3k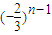），Sn=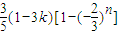要使a＜Sn＜b对任意正整数n成立，即
∴
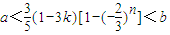
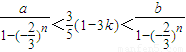
令g（n）=
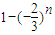
当n为正奇数时，
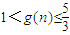；当n为正偶数时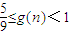，∴g（n）的最大值为g（1）=
，最小值为g（2）=∴
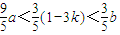
∴3a＜1-3k＜b
∴
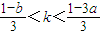
∴当a＜b≤3a时，
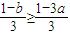，不存在实数k满足条件；当b＞3a时，
，存在实数k，使得对任意正整数n，都有a＜Sn＜b，且k的取值范围为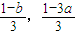（）．点评：本题考查函数的单调性，考查函数的性质，考查赋值法的而运用，考查存在性问题的探究，属于中档题．
练习册系列答案
相关题目