题目内容
已知以点 为圆心的圆与直线
为圆心的圆与直线 相切.过点
相切.过点 的动直线
的动直线 与圆
与圆 相交于
相交于 两点,
两点, 是
是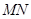 的中点.
的中点.
(1)求圆 的方程;
的方程;
(2)当 时,求直线
时,求直线 的方程.(用一般式表示)
的方程.(用一般式表示)
(1) (2)
(2) 或
或
解析试题分析:(1)设圆 的半径为
的半径为 ,
, 由于圆
由于圆 与直线
与直线 相切,
相切,
∴
∴圆A的方程为
(2)①当直线 与
与 轴垂直时,易知
轴垂直时,易知 符合题意;
符合题意;
②当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为
即
连接 ,则
,则
∵ ∴
∴
则由 ,得
,得
∴直线
故直线 的方程为
的方程为 或
或
考点:圆的标准方程及直线与圆相交相切的位置关系
点评:直线与圆相切:圆心到直线的距离等于半径;直线与圆相交:圆心到直线的距离,圆的半径,弦长的一半构成直角三角形

练习册系列答案
相关题目
 ,直线
,直线 与圆
与圆 相交于
相交于 两点,且A点在第一象限.
两点,且A点在第一象限. ;
; (
( )是圆
)是圆 关于原点的对称点为
关于原点的对称点为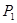 ,点
,点 轴的对称点为
轴的对称点为 ,如果直线
,如果直线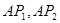 与
与 轴分别交于
轴分别交于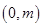 和
和 .问
.问 是否为定值?若是,求出定值,若不是,说明理由.
是否为定值?若是,求出定值,若不是,说明理由.  过点
过点 ,且与直线
,且与直线 相切于点
相切于点 .
.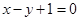 对称的圆
对称的圆 的方程.
的方程.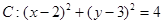 ,直线
,直线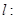
 ,
,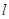 与圆
与圆 恒相交;
恒相交; 时,过圆
时,过圆 作圆的切线
作圆的切线 交直线
交直线 点,
点, 为圆
为圆 的取值范围;
的取值范围; .
. 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求 的取值范围.
的取值范围. 的极坐标方程是
的极坐标方程是 ,曲线
,曲线 的参数方程是
的参数方程是 是参数).
是参数). 的取值范围,使得
的取值范围,使得 上,与
上,与 轴相切,且被直线
轴相切,且被直线 截得弦长为
截得弦长为 的圆的方程.
的圆的方程.  相切于点
相切于点 .
. 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.  轴相切,圆心在直线
轴相切,圆心在直线 上,且在直线
上,且在直线 上截得的弦长为
上截得的弦长为 ,求圆C的方程.
,求圆C的方程.