题目内容
18．已知△ABC中，内角A、B、C的对边的边长为a、b、c，且bcosC=（2a-c）cosB，则y=1+2cos2B的值为0．分析 由条件利用正弦定理化简可得sin（B+C）=2sinAcosB，求得cosB=$\frac{1}{2}$，可得B=$\frac{π}{3}$，由此求得y=1+2cos2B的值．
解答 解：△ABC中，bcosC=（2a-c）cosB，利用正弦定理可得sinBcosC=2sinAcosB-sinCcosB，
化简可得sin（B+C）=2sinAcosB，求得cosB=$\frac{1}{2}$，可得B=$\frac{π}{3}$，
则y=1+2cos2B=1-1=0，
故答案为：0．
点评 本题主要考查正弦定理的应用，两角和的正弦公式，属于基础题．
练习册系列答案
相关题目
9．
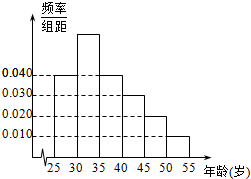某高校经济管理学院在2014年11月11日“双11购物节”期间，对[25，55]岁的人群随机抽取了100人进行调查，得到各年龄段人数频率分布直方图．同时对这100人是否参加“商品抢购”进行统计，结果如下表：
（1）求统计表中a和p的值；
（2）从年龄落在（40，50]内的参加“商品抢购”的人群中，采用分层抽样法抽取6人参加满意度调查，在抽取的6人中，有随机的2人感到“满意”，设感到“满意”的2人中年龄在（40，45]内的人数为X，求X的分布列和数学期望．
（3）通过有没有95%的把握认为，进行“商品抢购”与“年龄低于40岁”有关？说明你的理由．
附：K2=$\frac{n（ad-bc）2}{（a+b）（c+d）（a+c）（b+d）}$
某高校经济管理学院在2014年11月11日“双11购物节”期间，对[25，55]岁的人群随机抽取了100人进行调查，得到各年龄段人数频率分布直方图．同时对这100人是否参加“商品抢购”进行统计，结果如下表：（1）求统计表中a和p的值；
（2）从年龄落在（40，50]内的参加“商品抢购”的人群中，采用分层抽样法抽取6人参加满意度调查，在抽取的6人中，有随机的2人感到“满意”，设感到“满意”的2人中年龄在（40，45]内的人数为X，求X的分布列和数学期望．
（3）通过有没有95%的把握认为，进行“商品抢购”与“年龄低于40岁”有关？说明你的理由．
| 组数 | 分组 | 抢购商品的人数 | 占本组的频率 |
| 第一组 | [25，30） | 12 | 0.6 |
| 第二组 | [30，35） | 18 | p |
| 第三组 | [35，40） | 10 | 0.5 |
| 第四组 | [40，45） | a | 0.4 |
| 第五组 | [45，50） | 3 | 0.3 |
| 第六组 | [50，55） | 1 | 0.2 |
| P（χ2≥k） | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
6．命题P：不等式lg[x（1-x）+1]＞0的解集为{x|0＜x＜1}，
命题q：在△ABC中，A＞B是${cos^2}（{\frac{A}{2}+\frac{π}{4}}）＜{cos^2}（{\frac{B}{2}+\frac{π}{4}}）$成立的必要不充分条件，
则 下列说法正确的是（ ）
命题q：在△ABC中，A＞B是${cos^2}（{\frac{A}{2}+\frac{π}{4}}）＜{cos^2}（{\frac{B}{2}+\frac{π}{4}}）$成立的必要不充分条件，
则 下列说法正确的是（ ）
| A． | P真q假 | B． | p∧q为真 | C． | p∨q为假 | D． | P假q真 |
13．正项等比数列{an}中，a6-a4=24，a3a5=64，则{an}的前8项和为（ ）
| A． | 63 | B． | 127 | C． | 128 | D． | 255 |
3．定义在R上的函数f（x）满足f（x+1）=2f（x），且当x∈（0，1）时，f（x）=4x，则f（5.5）=（ ）
| A． | 32 | B． | $\frac{129}{4}$ | C． | 64 | D． | 16 |