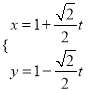题目内容
【题目】已知函数y=f（x）在R上为奇函数，当x＞0时，f（x）=3x2﹣9，则f（﹣2）=
【答案】﹣3
【解析】解：由题意：函数y=f（x）在R上为奇函数，可得：f（0）=0，f（﹣x）=﹣f（x）．
当x＞0时，f（x）=3x2﹣9，
当x＜0时，则﹣x＞0，f（﹣x）=3x2﹣9，
∵f（﹣x）=﹣f（x），
∴f（x）=﹣3x2+9，
故得f（x）在R上解析式为：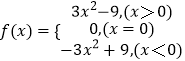 
，
∵﹣2＜0，
∴f（﹣2）=﹣3（﹣2）2+9=﹣3．
所以答案是：﹣3．
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点，需要掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇才能正确解答此题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某经销商从外地一水殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如下图：
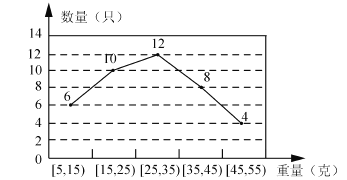
（1）记事件
为：“从这批小龙虾中任取一只，重量不超过35
的小龙虾”，求
的估计值；
（2）试估计这批小龙虾的平均重量；
（3）为适应市场需求，制定促销策略．该经销商又将这批小龙虾分成三个等级，并制定出销售单价，如下表：
等级 | 一等品 | 二等品 | 三等品 |
重量（ |
|
|
|
单价（元/只） | 1.2 | 1.5 | 1.8 |
试估算该经销商以每千克至多花多少元（取整数）收购这批小龙虾，才能获得利润？
