Question

【题目】已知函数f（x）=|2x﹣1|﹣x，
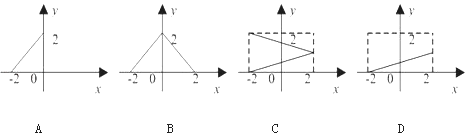
（1）用分段函数的形式表示该函数，并画出该函数的图象；
（2）写出该函数的值域、单调区间（不要求证明）；
（3）若对任意x∈R，不等式|2x﹣1|≥a+x恒成立，求实数a的取值范围．

Answer 1

【答案】
（1）解：∵函数f（x）=|2x﹣1|﹣x= ，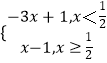

函数的图象如下图所示：

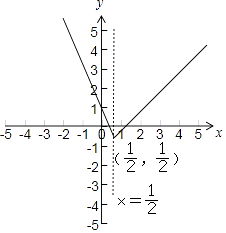
（2）解：由图可得：函数的值域为：[﹣ ，+∞）；

单调减区间为：为：（﹣∞， ]，单调增区间为：[ ，+∞）

（3）解：若对任意x∈R，不等式|2x﹣1|≥a+x恒成立，

则a≤|2x﹣1|﹣x恒成立，

即a≤﹣

【解析】（1）利用零点分段法，可将函数解析式化为分段函数，进而结合一次函数的图象和性质，得到函数的图象；（2）数形结合，可得函数的值域、单调区间；（3）若对任意x∈R，不等式|2x﹣1|≥a+x恒成立，则a≤|2x﹣1|﹣x的最小值．