题目内容
【题目】(本小题满分14分)
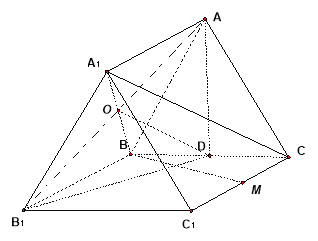
在正三棱柱![]() 中,点
中,点![]() 是
是![]() 的中点,
的中点,![]() .
.
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)试在棱![]() 上找一点
上找一点![]() ,使
,使![]() .
.
【答案】(1)详见解析(2)![]() 为
为![]() 的中点.
的中点.
【解析】
试题分析:(1)证明线面平行,一般利用线面平行判定定理进行证明,即先从线线平行出发,这可利用三角形中位线性质进行证明:连接![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,所以
的中点,所以![]() ∥
∥![]() .从而可证
.从而可证![]() ∥平面
∥平面![]() .(2)找一点目的是证线线垂直,故从垂直角度找:利用正方形性质,边的中点与对边顶点连线存在垂直关系,故取
.(2)找一点目的是证线线垂直,故从垂直角度找:利用正方形性质,边的中点与对边顶点连线存在垂直关系,故取![]() 为
为![]() 的中点.再根据线面垂直判定及性质定理进行论证.
的中点.再根据线面垂直判定及性质定理进行论证.
试题解析:(1)证明:连接![]() ,交
,交![]() 于点
于点![]() , 连接
, 连接![]() .
.
∵![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() ∥
∥![]() . 3分
. 3分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() . 6分
. 6分
(2)![]() 为
为![]() 的中点. 7分
的中点. 7分
证明如下:
∵在正三棱柱![]() 中,
中,![]() ,∴四边形
,∴四边形![]() 是正方形.
是正方形.
∵![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 的中点,∴
的中点,∴![]() , 9分
, 9分
∴![]() ,
,![]() .
.
又∵![]() ,
,
![]() ,∴
,∴![]() . 11分
. 11分
∵![]() 是正三角形,
是正三角形,![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
∵平面![]() 平面
平面![]() , 平面
, 平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]()
![]() . 13分
. 13分
∵![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() . 14分
. 14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如表:
x | ﹣ |
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果:
( i)当x∈[0, ![]() ]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
( ii)若α,β是锐角三角形的两个内角,试比较f(sinα)与f(cosβ)的大小.
