题目内容
4.已知函数f(x)=ln(ax+1)+x2-ax-m(a>0).(1)求函数f(x)的单调区间;
(2)当a=1时,函数f(x)存在3个零点x1,x2,x3,设x1<x2<0<x3,求m的取值范围.
分析 (1)求导,利用导函数的正负判断函数的单调性,利用二次函数对参数进行讨论.
(2)求导,利用导函数判断函数的极值,利用极值模拟函数图象,结合函数零点的个数得出极值的范围.
解答 解:(1)f′(x)=$\frac{a}{ax+1}$+2x-a=$\frac{2a{x}^{2}+2x-{a}^{2}x}{ax+1}$ 函数的定义域为(-$\frac{1}{a}$,+∞)
当a>$\sqrt{2}$时
在(-$\frac{1}{a}$,0),( $\frac{{a}^{2}-2}{2a}$,+∞)上,f′(x)>0,f(x)是增函数,
在(0,$\frac{{a}^{2}-2}{2a}$)f′(x)<0,f(x)是减函数.
当a=$\sqrt{2}$时,f(x)在(-$\frac{\sqrt{2}}{2}$,+∞)是增函数.
当0<a<$\sqrt{2}$时
在(-$\frac{1}{a}$,$\frac{{a}^{2}-2}{2a}$),( 0,+∞)上,f′(x)>0,f(x)是增函数,
f(x)在($\frac{{a}^{2}-2}{2a}$,0)上,f′(x)<0,f(x)是减函数.
(2)当a=1时,f(x)=ln(x+1)+x2-x-m
f′(x)=$\frac{x(2x+1)}{x+1}$
令f′(x)=0得:x=0和x=-$\frac{1}{2}$
在(-1,-$\frac{1}{2}$),(0,+∞)f′(x)>0,f(x)递增,
在(-$\frac{1}{2}$,0)上,f′(x)<0,f(x)递减,
∴f(-$\frac{1}{2}$)为极大值,f(0)为极小值
若使函数f(x)存在3个零点x1,x2,x3,设x1<x2<0<x3
则:f(-$\frac{1}{2}$)>0且f(0)<0
∴0<m<$\frac{3}{4}$-ln2
点评 考察了利用导函数判断函数的单调性,对二次函数参数的讨论问题,极值的判断和对题意的理解.

 中考解读考点精练系列答案
中考解读考点精练系列答案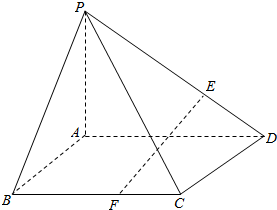 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a.点E、F分别在PD、BC上,且PE:ED=BF:FC
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a.点E、F分别在PD、BC上,且PE:ED=BF:FC