题目内容
9.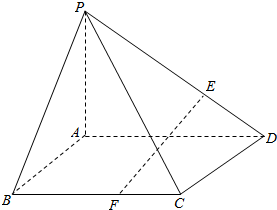 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a.点E、F分别在PD、BC上,且PE:ED=BF:FC
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a.点E、F分别在PD、BC上,且PE:ED=BF:FC(1)求证:PA⊥平面ABCD;
(2)求证:EF∥平面PAB.
分析 (1)由底面是菱形,加上∠ABC=60°,又对角线AC=a,可以得到菱形的边长为a,这样PAB,PAD由三边长就可以得到∠PAB与∠PAD是直角,线面垂直得证.
(2)经F点作AB的平行线交AD于M点,连接EM,由比例关系可证EM∥PA,由平面EFM∥平面PBA,EF?平面EFM即可证明EF∥平面PAB.
解答 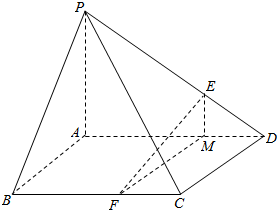 证明:(1)∵底面ABCD是菱形,∠ABC=60°,AC=a,
证明:(1)∵底面ABCD是菱形,∠ABC=60°,AC=a,
∴菱形的边长为a,
∵PB=PD=$\sqrt{2}$a.
∴PA2+AB2=PB2,PA2+AB2=PD2,
∴由勾股定理可得:PA⊥BA,PA⊥AD,又AB∩AD=A,
∴PA⊥平面ABCD.
(2)经F点作AB的平行线交AD于M点,连接EM,
∵FM∥AB,
∴BF:FC=AM:MD,
∵PE:ED=BF:FC,
∴PE:ED=AM:MD,
∴EM∥PA,
∴平面EFM∥平面PBA,EF?平面EFM,
∴EF∥平面PAB.
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查了空间想象能力和推理论证能力,属于基本知识的考查.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目