题目内容

F是双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的一个焦点，过F作直线l与一条渐近线平行，直线l与双曲线交于点M，与y轴交于点N，若
FM
=
1
2
MN
，则双曲线的离心率为（　　）
A．
2
B．
3
C．
5
D．
10
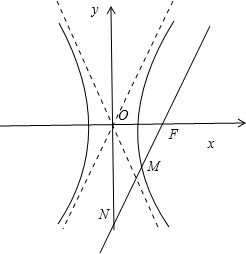
如图所示，
∵过F作直线l与一条渐近线平行，
∴直线l的方程为y=
b
a
(x-c)，
联立
y=
b
a
(x-c)
x2
a2
-
y2
b2
=1
，化为x=
a2+c2
2c
，．
∵
FM
=
1
2
MN
，
∴
a2+c2
2c
-c=-
1
2
a2+c2
2c
，
化为c2=3a2，
解得e=
c
a
=
3
．
故选：B．
练习册系列答案
相关题目
已知双曲线
x2
36
-
y2
45
=1上一点P到焦点F1的距离是16，则P到F2的距离是______．
已知Fz、F2是双曲线
x2
a2
-
y2
b2
=z(a＞a，b＞a)的两个焦点，P是双曲线上的一点，则
PFz
•
PF2
的取值范围是______．
设F1，F2是双曲线x2-
y2
4
=1的左、右两个焦点，若双曲线右支上存在一点P，使（
OP
+
OF2
）•
F2P
=0（O为坐标原点），且|PF1|=λ|PF2|，则λ的值为______．
图中两个两条双曲线的离心率分别是e1、e2，且e1＜e2，则曲线C1的离心率是______，曲线C2的离心率是______．
如果圆锥曲线
y2
λ+5
-
x2
2-λ
=1的焦距与实数λ无关，那么它的焦点坐标是______．
设F1，F2是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两个焦点．若在C上存在一点P．使PF1⊥PF2，且∠PF1F2=30°，则C的离心率为______．
过双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左焦点F1（-2，0）、右焦点F2（2，0）分别作x轴的垂线，交双曲线的两渐近线于A、B、C、D四点，且四边形ABCD的面积为16
3
．
（1）求双曲线C的标准方程；
（2）设P是双曲线C上一动点，以P为圆心，PF2为半径的圆交射线PF1于M，求点M的轨迹方程．
过抛物线y2＝2px(p>0)的焦点F作倾斜角为45°的直线交抛物线于A，B两点，若线段AB的长为8，则p＝________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网