题目内容
【题目】如图,四面体ABCD中,平面DAC⊥底面ABC,![]() ,AD=CD=
,AD=CD=![]() ,O是AC的中点,E是BD的中点.
,O是AC的中点,E是BD的中点.
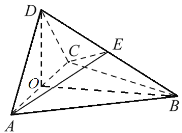
(1)证明:DO⊥底面ABC;
(2)求二面角D-AE-C的余弦值.
【答案】(1)见解析;
(2)![]() .
.
【解析】
(1)根据等腰三角形的性质得到![]() ,在根据面面垂直的性质定理,证得
,在根据面面垂直的性质定理,证得![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点建立空间直角坐标系,利用平面
为坐标原点建立空间直角坐标系,利用平面![]() 和平面
和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值.
的余弦值.
(1)证明:∵ AD=CD=![]() ,O是AC的中点,
,O是AC的中点,
∴ DO⊥AC.
∵ 平面DAC⊥底面ABC,平面DAC∩底面ABC=AC,
∴ DO⊥底面ABC.
(2)解:由条件易知DO⊥BO,BO⊥AC.
OA=OC=OD=2, OB=![]()
如图,以点O为坐标原点,OA为x轴, OB为y轴,OC为z轴建立空间直角坐标系.
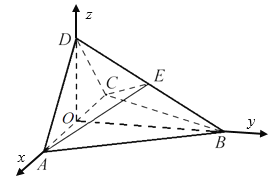
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面ADE的一个法向量为![]() ,
,
则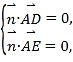 即
即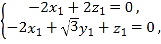
令![]() ,则
,则![]() ,所以
,所以![]() .
.
同理可得平面AEC的一个法向量![]() .
.
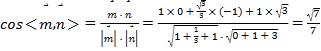 .
.
因为二面角D-AE-C的平面角为锐角,所以二面角D-AE-C的余弦值为![]() .
.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目