题目内容
【题目】设动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,记![]() =λ.当∠APC为钝角时,λ的取值范围是________.
=λ.当∠APC为钝角时,λ的取值范围是________.
【答案】(![]() ,1)
,1)
【解析】
本题主要考查了用空间向量求直线间的夹角,一元二次不等式的解法,意在考查考生的空间想象能力以及运算求解能力.
以![]() 、
、![]() 、
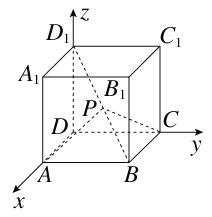
、![]() 为单位正交基底,建立如图所示的空间直角坐标系D-xyz,则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),则
为单位正交基底,建立如图所示的空间直角坐标系D-xyz,则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),则![]() =(1,1,-1),得
=(1,1,-1),得![]() =λ
=λ![]() =(λ,λ,-λ),所以
=(λ,λ,-λ),所以![]() =
=![]() +
+![]() =(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),
=(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),![]() =
=![]() +
+![]() =(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1),显然∠APC不是平角,所以∠APC为钝角等价于
=(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1),显然∠APC不是平角,所以∠APC为钝角等价于![]() ·
·![]() <0,即-λ(1-λ)-λ(1-λ)+(λ-1)2<0,即(λ-1)(3λ-1)<0,解得
<0,即-λ(1-λ)-λ(1-λ)+(λ-1)2<0,即(λ-1)(3λ-1)<0,解得![]() <λ<1,因此λ的取值范围是(
<λ<1,因此λ的取值范围是(![]() ,1).
,1).

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
【题目】某校高一某班50名学生参加防疫知识竞赛,将所有成绩制作成频率分布表如下:
分组 | 频数 | 频率 |
|
|
|
|
| 0.06 |
| 35 | 0.070 |
| 6 | 0.12 |
| 4 |
|
(1)求频率分布表中![]() 的值;
的值;
(2)从成绩在![]() 的学生中选出2人,请写出所有不同的选法,并求选出2人的成绩都在
的学生中选出2人,请写出所有不同的选法,并求选出2人的成绩都在![]() 中的概率.
中的概率.