题目内容
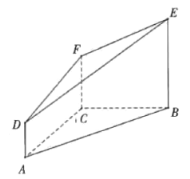
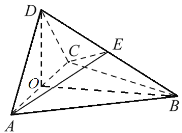
【题目】正方体![]() 的棱长为
的棱长为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,则过
的中点,则过![]() 且与
且与![]() 平行的平面截正方体所得截面的面积为______,
平行的平面截正方体所得截面的面积为______,![]() 和该截面所成角的正弦值为______.
和该截面所成角的正弦值为______.
【答案】![]()
![]()
【解析】
取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,推导出平面
,推导出平面![]() 平面
平面![]() ,过
,过![]() 且与
且与![]() 平行的平面截正方体所得截面为
平行的平面截正方体所得截面为![]() ,由此能求出过
,由此能求出过![]() 且与
且与![]() 平行的平面截正方体所得截面的面积;以
平行的平面截正方体所得截面的面积;以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能求出
轴,建立空间直角坐标系,利用向量法能求出![]() 和该截面所成角的正弦值.
和该截面所成角的正弦值.
取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∴过![]() 且与
且与![]() 平行的平面截正方体所得截面为
平行的平面截正方体所得截面为![]() ,
,
∵![]() ,
,![]() ,四边形
,四边形![]() 是矩形,
是矩形,
∴过![]() 且与
且与![]() 平行的平面截正方体所得截面
平行的平面截正方体所得截面![]() 的面积为:
的面积为:
![]() ;
;
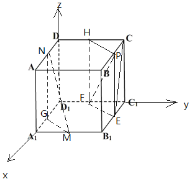
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则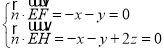 ,取
,取![]() ,得
,得![]() ,
,
设![]() 和该截面所成角为
和该截面所成角为![]() ,
,
则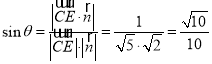 ,
,
∴![]() 和该截面所成角的正弦值为
和该截面所成角的正弦值为![]() .
.
故答案为:![]() ;
;![]() .
.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.

甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
![]() 现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(II)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
下面临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | .024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2=![]() )
)
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中不可或缺的一部分![]() 市某调查机构针对该市市场占有率最高的两种网络外卖企业
市某调查机构针对该市市场占有率最高的两种网络外卖企业![]() 以下简称外卖A、外卖
以下简称外卖A、外卖![]() 的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
分数 人数 种类 |
|
|
|
|
|
外卖A | 50 | 150 | 100 | 400 | 300 |
外卖B | 100 | 100 | 300 | 200 | 300 |
表中得分越高,说明市民对网络外卖服务越满意![]() 若得分不低于60分,则表明该市民对网络外卖服务质量评价较高
若得分不低于60分,则表明该市民对网络外卖服务质量评价较高![]() 现将分数按“服务质量指标”划分成以下四个档次:
现将分数按“服务质量指标”划分成以下四个档次:
分数 |
|
|
|
|
服务质量指标 | 0 | 1 | 2 | 3 |
视频率为概率,解决下列问题:
![]() 从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
![]() 从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
![]() 在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.